|
|
1.IntroductionHyperspectral images are collected by sensors on a very high number of wavelengths forming a three-dimensional cube. These cubes represent a large amount of data and are usually acquired on board a satellite and sent afterward to a ground station. The available transmission bandwidths are limited; hence an efficient compression is usually necessary. Hyperspectral images, as most scientific data, have been traditionally compressed by means of lossless methods. An example of these is the recent standard for lossless hyperspectral image compression developed by the Consultative Committee for Space Data Systems.1 However, lossy compression of hyperspectral images has recently become very popular as it can achieve higher compression ratios. Among the already proposed methods for lossy hyperspectral image compression, it is possible to find generalizations of existing two-dimensional image or video compression algorithms.2–5 Although these techniques achieve satisfactory performance, the existing compression standards are usually too complex to be implemented on the on-board hardware. Therefore, some algorithms have been specifically designed for on-board compression in order to reduce the computational and memory resources requirements. Therefore, for this work, we consider the algorithm presented in Ref. 6, which was proposed for the European Space Agency’s Exomars mission and is in the following referred to as lossy compression for Exomars (LCE). The primary motivation for opting for this algorithm is that it meets several requirements that are crucial for on-board compression, such as low complexity and error resilience. Moreover, it was designed in such a way that it can be easily parallelized in order to speed up the compression process for high-data-rate sensors. In addition to proposing new methods for on-board data compression, it is also mandatory to take into consideration the hardware where the algorithms are physically implemented and executed. In this sense, nowadays graphics processing units (GPUs) represent a very attractive opportunity, offering the possibility to dramatically increase the computation speed in data and task-parallel applications, which is the case of certain types of hyperspectral data compression methods. We note that GPUs cannot be used for on-board compression yet because of their large size, power consumption, and not being radiation-tolerant; however, the performance improvements obtained when GPUs are utilized for satellite image processing have already been addressed for different applications, including compression.7–10 The LCE algorithm is inherently data and task-parallel; therefore during this exploration, it is implemented on a GPU using Nvidia computer unified device architecture (CUDA) parallel computing architecture11 in order to demonstrate the feasibility of GPUs for remote sensing applications and contribute to identify and propose solutions to the the potential difficulties commonly encountered when trying to accelerate algorithms for hyperspectral image compression, if space-qualified GPUs become a reality in the near future. Promising results have already been shown in Ref. 7, and Ref. 12, where a GPU implementation of a lossless compression algorithm for on-board compression is presented. These previous studies serve as a motivation to continue exploring the capabilities of parallel processing applied to on-board processing, showing how well a lossy compression algorithm specifically designed for on-board compression would perform on a GPU and providing a profiling and performance evaluation. A CUDA implementation of the different compression stages of the LCE algorithm is presented, with a detailed description of the parallelization of the entropy coding and bit packing phases of the algorithm, for which a more sophisticated strategy is needed due to the existing data dependencies. Several experimental results are designed in order to show the performance of the GPU implementation of the algorithm, comparing it with a single-threaded CPU implementation. Moreover, the accuracy of the GPU implementation is addressed, as well as the influence of the user-defined configuration parameters of the LCE algorithm on the performance. The remainder of this paper is organized as follows: Secs. 2 and 3 present the LCE algorithm and its software implementation, respectively. A brief description of the GPU architecture and Nvidia CUDA is given in Sec. 4 and the parallelization strategy for the LCE algorithm is presented in Sec. 5. Finally, Sec. 6 shows the experimental result and Sec. 7 draws the conclusions. 2.Lossy Compression for Exomars AlgorithmThe LCE algorithm6 was specifically designed to be able to perform on-board compression, achieving high coding efficiency and meeting other very important requirements for on-board compression at the same time, namely low complexity, error resilience, and hardware friendliness. The algorithm applies a scheme consisting of a prediction plus a Golomb power-of-two entropy coder. It partitions the data into units, which are portions of the hyperspectral cube of size pixels with all bands and can be compressed independently. The different stages of the LCE algorithm are explained below. 2.1.PredictionThe algorithm compresses independent nonoverlapping spatial blocks of size with all bands in the hyperspectral cube, which are processed separately. In the following, denotes the pixel of a hyperspectral image sample in the ’th line, ’th column, and ’th band. For the first band (), 2-D compression is performed using a predictor defined as , where denotes the predictor, denotes the decoded value, and stands for right shift. For all other bands, the samples are predicted from the decoded samples in the previous band. The predicted values are computed for all samples in a block as , where stands for quantized least-square estimator and and represent the average value of the colocated decoded blocks in band and , respectively. Finally, the prediction error is computed as . 2.2.Rate-Distortion OptimizationOnce the prediction error samples are obtained, they are quantized. With the purpose of obtaining higher compression ratios and reducing the number of computations, the algorithm checks if the prediction is so close to the actual pixel values that it makes sense to skip the encoding of the prediction error samples. Instead, a one-bit flag is raised, indicating that the prediction error samples of the current block are all zero. 2.3.Quantization and MappingThe prediction error samples are quantized to integer values and dequantized to reconstructed values . For the first band, this process is performed pixel by pixel using a scalar uniform quantizer. For the other bands, it is possible to choose between a scalar uniform quantizer and a uniform-threshold quantizer (UTQ).13 Finally, the reconstructed values are mapped to non-negative values. 2.4.Entropy CodingThe residuals of a block are encoded in raster order using a Golomb code14 whose parameter is constrained to a power of two, except for the first sample of each block, which is encoded using an exponential Golomb code of order zero. The quantized first sample of the first band is not encoded and saved to the compressed file with 16 bits. The compressed file is a concatenation of coded blocks, which are read spatially in raster order, and each block is coded with all bands. 3.Software Implementation of the LCE AlgorithmThe LCE algorithm was originally implemented in C programming language, to be executed on a single-threaded CPU. It operates independently in every block with all its bands. For the specific case of this study, we consider a block size of , which as stated in Ref. 6 typically optimizes the algorithm performance. Each block in the image is identified with two coordinates in the horizontal and vertical spatial directions, namely and . In the following, denotes a pixel block in coordinates and band . A single pixel in is denoted as . Additionally, and are the total number of blocks that can be found in the image in the horizontal and vertical spatial dimension. The LCE compressor consists basically of a chained loop, which iterates to cover all horizontal and vertical blocks in the image, and all bands in a block. The innermost loop reads a block and performs the different stages of the LCE algorithm presented in Sec. 2 for every single pixel , namely the prediction, rate-distortion optimization, quantization, entropy coding, and bit packing to create the compressed file. The pseudocode showing the chained loop and the different compression stages is shown in Fig. 1. 3.1.Generation of the Compressed FileThe result of the previously described chained loop is a bit stream that represents the compressed image. The codewords resulting from the entropy coding stage are written by the software in a single file, in the same order that they are obtained. Since Golomb codes produce codewords of variable length, they are buffered in a bit-by-bit fashion to a 32-bit variable. When the buffer is full, it is written to the compressed file, generating the bit stream. 3.2.Configuration ParametersThe software implementation allows the user to configure the algorithm by selecting different parameters to set the functionality mode (baseline or advanced) and the quality of the resulting compressed image. The baseline algorithm performs compression using a scalar quantizer, fully implemented with integer arithmetic; an advanced algorithm replaces the scalar quantizer with the UTQ,13 which uses floating-point arithmetic. The parameter UTQ can be set by the user to select the functionality mode. Setting enables the UTQ quantizer and setting uses the baseline functionality mode. The quality of the resulting compressed image can also be set by the user by assigning values to a parameter named delta, making it possible to find a trade-off between quality and bit rate. Delta sets the quantization step size of the quantizer; therefore, increasing delta yields higher compression ratios, but lower quality of the reconstructed image. Delta has to be an integer , with providing the maximum possible quality. 4.GPU Architecture and Nvidia CUDAGPUs are structured as a set of multiprocessors, each composed of a set of simple processing elements working in single-instruction multiple data mode. The use of GPUs for general-purpose computation has become popular recently, as well as the computer architecture developed by Nvidia named CUDA.11 This architecture provides a scalable programming model and a software environment for parallel computing, including a set of application programming interfaces, which makes it possible to manage the device and its memory, but hides the real hardware from the developers. The function that is executed in parallel is typically called a kernel. A CUDA kernel executes in parallel across a set of parallel threads. The programmer organizes these threads into a hierarchy of grids of blocks. A CUDA block is a set of concurrent threads that can cooperate among themselves. The grid is the set of blocks, which may be executed independently. The number of blocks and threads is set by the programmer in the kernel call. The necessary data has to be made available for the GPU by copying it from the CPU. Threads may access different memory spaces during their execution. Each single thread has a private local memory consisting of registers (low-latency on-chip memory) private to each thread. Shared memory is partitioned in such a way that it is visible and accessible for all threads in a specific block. This makes it possible for threads to exchange information and cooperate among themselves. Finally, global memory is visible to all threads of all blocks, and it is allocated in the high-latency DRAM of the GPU. 5.Parallelization of the LCE Compressor with CUDAIn order to parallelize the LCE compressor to implement it on a GPU, several facts are considered, specifically:
Several parallel kernels are designed to perform the different stages of the LCE algorithm. One performs the prediction, rate-distortion optimization, and mapping, conserving the existing dependency between bands. A separate one, for which more parallelization can be obtained, accomplishes the entropy coding stage, and finally, a third one executes the bit packing and creates the final compressed bit stream. The number of CUDA threads and blocks called in each kernel is established in such a way that the CUDA application is suitable to compress any hyperspectral image, regardless of its spatial or spectral size in short compression times. Nevertheless, the presented kernel dimensionality might be further optimized for a specific image, taking into consideration its size and adjusting the number of threads and blocks accordingly. Before parallelizing an algorithm using the CUDA abstractions, the user has to take into account the limitations of the GPU where it is going to be executed. Specifically, the main limitations refer to the amount of dedicated memory storage, computation capability, and maximum number of CUDA blocks and threads that can be launched by a single kernel. In this exploration, the LCE algorithm is implemented in an Nvidia Tesla C2075 GPU and a GeForce GTX 480, which have 6144 and 1536 MB of dedicated memory, respectively, and both restrict the number of CUDA blocks and threads to a maximum of 65,535 and 1024, respectively. 5.1.Allocation of the Image Data in the GPUThe necessary image data have to be sent and stored to the GPU dedicated memory in order to make it possible to perform operations on them. It is decided to copy the whole hyperspectral cube to the GPU before executing any of the kernels in order to minimize the number of transactions between the CPU and GPU. Once the necessary data are stored in the GPU, an efficient use of the different memory spaces is necessary to hide latency. When data are copied from the CPU to the GPU, they are initially stored in the global memory; however, CUDA local or shared memory spaces are used whenever it is convenient to accelerate memory accesses. 5.2.Prediction, Rate-Distortion Optimization, Quantization, and MappingThe first kernel that is executed performs the aforementioned stages of the compression. As it was already stated, parallelization can be obtained by exploiting the fact that every block with all bands can be processed in parallel and that the samples can also be treated independently when spectral prediction is employed, i.e., for all bands except the first one. Therefore, as shown in the pseudocode of Fig. 2, the loops that iterate to cover all horizontal and vertical blocks can be executed in parallel. Besides, the loops that are used to cover all samples in a block in band can also be avoided, except for the first band. However, it is still necessary to keep the loop that covers all bands in a block. The designed CUDA parallel kernel will perform the prediction on every block with all bands in parallel; therefore, the number of CUDA blocks that will be launched will be calculated as . Each CUDA block will launch 256 threads, each of them able to access and perform operations on a sample of the image in parallel. The hyperspectral image is stored in CUDA global memory. As the threads are going to access the same sample many times, the necessary data are copied to the local memory to make accesses faster. Specifically, every iteration of the loop that covers all bands, a block, i.e., 256 samples, are copied from global to local memory. Local memory is only visible for a thread; however, there are times when not all operations can be performed independently on every . Particularly, the computation of some operations require the summation of all samples in a block. For these specific cases, CUDA shared memory is used, which is visible for all threads in the same block. Besides, in those situations where the use of sequential loops cannot be avoided, the number of iterations is reduced using tree reduction strategies. 5.3.Entropy CodingUnlike the prediction stage previously described, the entropy coding phase can be performed on every block of a specific band in parallel, without any information from neighbouring bands, which makes it possible to process more data in parallel. A kernel is designed to perform the entropy coding of the mapped prediction residuals, which processes each block of prediction residuals in parallel. For optimization purposes, it is established that each kernel launches the maximum number of possible threads allowed by the Tesla C2075 and GeForce GTX 480 GPUs, which is 1024. Therefore, the number of CUDA blocks to be launched can be calculated as . We note that the maximum number of CUDA blocks is limited to 65,535. If the number of CUDA blocks obtained with the previous equation is higher than this maximum, then the kernel has to be called more than once, which negatively affects performance. Setting the number of threads to the maximum also serves to minimize the number of CUDA blocks called and, therefore, reduces the impact of having to invoke the kernel repeatedly. Several facts are considered when designing the GPU implementation of the entropy coding stage:
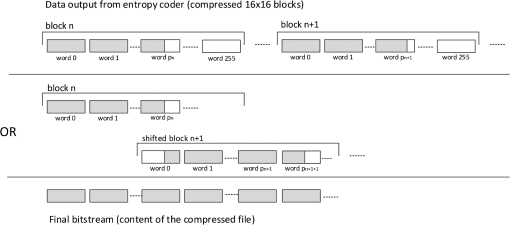
The strategy followed to generate the codewords and pack them to a bitstream must be different from the one followed in the CPU implementation, which is based on the sequential ordered generation of the codewords, as it is explained in Sec. 3. For the GPU implementation, the approach is to preprocess the Golomb parameters of all mapped prediction error samples in a block, and afterward compute the codewords for every sample in parallel. A strategy is designed to compute the Golomb parameter of every ’th sample of the block, , in parallel. This parameter is computed from a running count of the sum of the magnitude of the last 32 unmapped prediction errors of the block, ; for samples with index less than 32, only the available values are used. This implies that the Golomb parameter of a specific prediction error in a block depends on the accumulated sum of the previously unmapped prediction errors. The running count is obtained for every sample as . In order to be able to obtain in parallel, the prefix-sum of all the unmapped values is computed as . This is implemented in CUDA following the scheme proposed in Ref. 15, utilizing tree strategies to reduce the number of necessary iterations by taking advantage of CUDA shared memory. Once is known for every prediction error sample, the codewords can be created in parallel by the CUDA threads. Each thread computes and saves a codeword in its local memory. The size in bits of the obtained codewords is also saved by every thread, in order to be able to create the encoded buffer, as is explained in the following. The encoded prediction residuals have to be saved in raster order to produce the final encoded block, which contains the ordered sequence of codewords, without leaving any bits unused between them. The strategy presented in Ref. 16 is followed to write every codeword of a block in a single output buffer, as shown in Fig. 3. First, the final position of a codeword in the output buffer is calculated. This final position is given by two coordinates: the word position where the codeword is saved, word_position, and the bit position in that word where the codeword starts, starting_bit of every codeword. The result of the prefix-sum is the bit position of the codeword in the final output buffer. Dividing this result by 32 and obtaining the remaining yields the desired word_position and starting_bit. Once the two coordinates are calculated, the codewords are shifted in such a way that they start in the obtained starting_bit. Afterward, a logic OR is performed between the codewords with the same word_position, with CUDA atomic operations, which makes it possible for a thread to perform an operation without interference from any other threads, to avoid having threads with the same word_position accessing the output encoded buffer at the same time. 5.4.Bit Packing KernelOnce the encoded blocks corresponding to a pixel portion of the image are obtained, they have to be written to a single output buffer, which represents the compressed image. As each block has been processed independently in the entropy coding kernel, the resulting encoded blocks have been written to a specific position of the global memory. To construct the final output bit stream, the encoded blocks have to be saved in sequential order and, as it happened with the codewords, in such a way that no space is left unused between them. A strategy similar to the one used by the entropy coder is followed: the word position and starting bit is calculated for every compressed block. Afterward, the compressed block is shifted and an atomic OR is performed. However, this time it is necessary to perform the operations on complete encoded blocks (conformed by more than one 32-bit variable), which are allocated in the CUDA global memory, as shown in Fig. 4. Once again the word_position and starting_bit are obtained. This time they are computed for every encoded block. The blocks are copied from the global to the shared memory, where they are shifted according to the starting_bit in parallel. Finally the atomic operations are used to perform the logic OR and create the compressed bit stream. 6.Experimental ResultsDifferent experimental results are designed to evaluate the performance of the GPU implementation of the LCE algorithm with respect to the software implementation executed on a single-threaded CPU. The Nvidia Tesla C2075 is used to execute the CUDA implementation of the LCE algorithm. All the experiments are performed on a 3.19-GHz Intel Xeon W5580, running on a 64-bit operating system with 12 GB of RAM. Two different GPUs are used to execute the CUDA implementation of the LCE algorithm, an Nvidia Tesla C2075 and a GeForce GTX 480. Both GPUs are based on the Fermi17 architecture. The most important features of these GPUs are shown in Table 1. The main difference between them is the amount of dedicated memory storage, which is much higher for the Tesla GPU. In the following experiments, only the Tesla GPU will be used to run the LCE algorithm for those images that need more dedicated memory than it is available in the GeForce GPU. Table 1Description of the GPUs used for compression.
The hyperspectral images targeted for compression throughout the experiments are as follows:
As in the software implementation, the GPU application performs all the operations using single-precision integer variables, except for the quantization stage, which needs double-precision floating point operations when the UTQ is enabled. 6.1.Accuracy of the GPU ImplementationBefore any experiment is performed, the accuracy of the GPU implementation is tested. For this purpose, the images are compressed and decompressed with the GPU and the CPU implementation. The resulting compressed files are compared bit by bit, demonstrating that the results of both implementations are identical. Furthermore, both implementations are compared in terms of
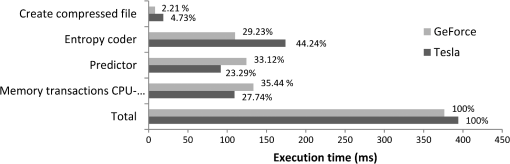
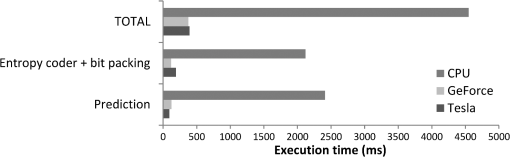
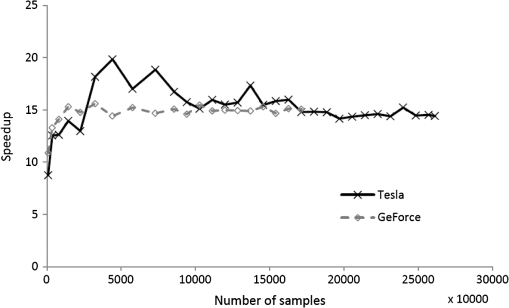
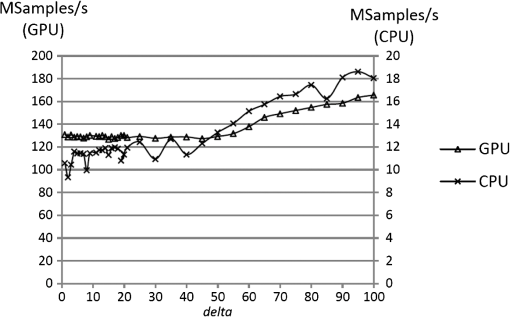
The aforementioned values were obtained for all images under evaluation, showing that there was no difference between the accuracy of the compression for the CPU and the GPU implementation. 6.2.Performance EvaluationIn order to evaluate the performance of the GPU implementation, the application is profiled by compressing a subimage of the AVIRIS cube of size comprising 220 bands. This hyperspectral cube is compressed with the GPU implementation and profiled with the tools supplied by Nvidia, in order to detect which of the kernels is the most time-consuming and where the main bottlenecks of the implementation are. The results in Fig. 5 show short compression times of 394 and 376 ms for the Tesla and GeForce GPU, respectively, which is almost a quarter of the time achieved with the GPU implementation of JPEG2000 presented in Ref. 18. The most time-consuming operations for both GPUs are the memory transactions between the CPU and the GPU. The strategy designed for the bit packing, which is used to create the final bit stream, shows very good performance, taking only 4.73% of the total compression time for the Tesla GPU and 2.21% for the GeForce GPU. Afterward, the computation time of the prediction and entropy coding and bit packing stages of the GPU implementation is compared with the same stages in the CPU implementation. The results in Fig. 6 show the high acceleration obtained with the GPU implementation in both stages. The strategy designed to parallelize the entropy coding and bit packing stages shows very good results. This stage is executed more than 10 times faster in the GPU than in the CPU. The performance of the GPU implementation of the LCE algorithm is also evaluated in terms of the speedup obtained with respect to the CPU implementation, which is calculated as . The speedup gives an idea of how many times the GPU execution is faster than that of the CPU. For a more accurate evaluation, several hyperspectral subimages are created with different spatial size, ranging from to the maximum possible size of the original images mentioned above. Figure 7 shows the speedup results for the AVIRIS image, against the total number of samples. The results obtained for both GPUs are similar. It can be observed that there are variations in the speedup obtained. The speedup is lower when the number of samples in the image—and hence the number of blocks that can be processed in parallel—is small. As the number of samples in the image increases, the speedup also increases until it becomes almost stable. Although the performance of the kernel initially increases with the number of samples, the time necessary to transfer data between GPU and CPU is proportional to the amount of samples in the image, which limits the possible speedup improvement. The observed peaks and slight variations of the speedup are caused by the fact that some combinations of spatial and spectral dimensions produce a more effective configuration of the CUDA kernels, resulting in a better performance of the GPU multiprocessors. This is more noticeable in the Tesla GPU, where higher speedup peaks are achieved. A similar curve was obtained for the AIRS and MODIS images. To summarize the speedup results, Table 2 shows the range of widths and lengths selected for generating the subsets of the hyperspectral images to be compressed, and the average speedup achieved. Table 2Average speedup obtained with the GPU implementation.
6.3.Effect of the Configuration Parameters on the PerformanceFinally, the effect of the configuration parameters of the LCE compressor on the performance of both implementations is presented. The parameters UTQ and delta can have an impact on the compression time of both the CPU and the GPU implementations of the algorithm. In the following, it is analyzed how the variation of these parameters affects the performance of the GPU implementation, with respect to the CPU implementation. Only the results obtained with the Tesla GPU are shown, because the results obtained with the GeForce were very similar. To evaluate the effect of varying UTQ, the set of images shown in Table 1 is compressed with the CPU and GPU implementation with and then with . Besides, two possible configuration parameters of delta are configured, namely , which provides the best possible results in terms of quality and the lowest compression ratio, and , which decreases the quality and increases the compression ratio. In order to better assess the effect of the parameters, the performance is evaluated in terms of the number of samples computed per second, calculated as . This value is calculated for all the subimages, and the average is computed. The results are summarized in Fig. 8. Fig. 8Effect of the configuration parameters of the LCE algorithm in the performance of the GPU implementation (a) and the CPU implementation (b). 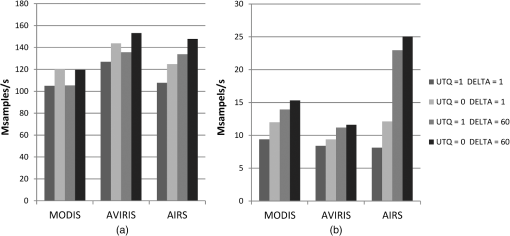 Both the GPU and CPU show better results when UTQ is disabled, since with UTQ enabled, double-precision operations have to be performed in the quantization stage of the LCE compressor. On the other hand, for parameter delta, it is observed that when delta is high, the performance improves, and this improvement is more noticeable in the CPU implementation, particularly for the AIRS image. This is explained by the fact that when delta is increased, the number of blocks that skip quantization is also high; therefore, the CPU implementation can avoid part of the operations and complete the processing of the image in a shorter time. Although the number of skipped blocks is the same for the GPU implementation, as data are processed in parallel, the fact that some of the blocks can be skipped does not make such a big difference in the processing time of the whole hyperspectral cube. To better depict this fact, in Fig. 9, the AVIRIS image with 220 bands is compressed with the CPU and the GPU implementation of the LCE algorithm for increasing values of delta, starting with up to . For both implementations, it can be observed that smaller compression times are achieved when delta is higher and that the number of samples computed per second for the GPU implementation is always around 10 times greater than the number of samples per second achieved by the CPU. It can be observed that the variation of the number of samples computed per second is more noticeable for the CPU implementation. However, even for great values of delta, the performance of the GPU is still significantly better than that of the CPU. 7.ConclusionsThe LCE algorithm is implemented on a GPU using Nvidia CUDA parallel architecture and compared with a software implementation executed on a single-threaded CPU in terms of accuracy of the results, compression speedup, and effect of the configuration parameters. A strategy is conceived in order to parallelize the different stages of the LCE algorithm to be executed in a GPU, with special emphasis on the acceleration of the entropy coding phase, where parallelization is crucial to obtain speedup. It is proved that the output bit stream produced by both implementations is identical. The GPU implementation shows short compression times, with an average speedup of up to 15.41 times the CPU compression time. The effect of the configuration parameters is also addressed, showing that the best performance results for the GPU are obtained when UTQ is disabled and the parameter delta is high. This study contributes to demonstrate that although GPUs are not suited to be used on-board a satellite, they still are very advantageous for hyperspectral image processing, including compression, when short execution times are desired, also providing very flexible implementations. AcknowledgmentsThis study has been partially funded by a Collaboration Grant given by the European Network of Excellence on High Performance and Embedded Architecture and Compilation (HiPEAC) network of excellence and TEC2011-28666.C04-04. ReferencesLossless Multispectral & Hyperspectral Image Compression. Blue Book Recommendation for Space Data System Standards, CCSDS 123.0-R-1,
(2012). Google Scholar
Q. DuJ. E. Fowler,
“Hyperspectral image compression using jpeg2000 and principal component analysis,”
IEEE Geosci. Rem. Sens. Lett., 4
(2), 201
–205
(2007). http://dx.doi.org/10.1109/LGRS.2006.888109 IGRSBY 1545-598X Google Scholar
A. KaramiM. YazdiG. Mercier,
“Compression of hyperspectral images using discrete wavelet transform and tucker decomposition,”
IEEE J. Sel. Topics Appl. Earth Observations Rem. Sens., 5
(2), 444
–450
(2012). http://dx.doi.org/10.1109/JSTARS.2012.2189200 1939-1404 Google Scholar
B. Pennaet al.,
“Transform coding techniques for lossy hyperspectral data compression,”
IEEE Trans. Geosci. Rem. Sens., 45
(5), 1408
–1421
(2007). http://dx.doi.org/10.1109/TGRS.2007.894565 IGRSD2 0196-2892 Google Scholar
L. Santoset al.,
“Performance evaluation of the h.264/avc video coding standard for lossy hyperspectral image compression,”
IEEE J. Sel. Topics Appl. Earth Observations Rem. Sens., 5
(2), 451
–461
(2012). http://dx.doi.org/10.1109/JSTARS.2011.2173906 1939-1404 Google Scholar
A. AbrardoM. BarniE. Magli,
“Low-complexity predictive lossy compression of hyperspectral and ultraspectral images,”
in IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP),
797
–800
(2011). Google Scholar
D. Keymeulenet al.,
“GPU lossless hyperspectral data compression system for space applications,”
in IEEE Aerospace Conf.,
1
–9
(2012). Google Scholar
V. FresseD. HouzetC. Gravier,
“GPU architecture evaluation for multispectral and hyperspectral image analysis,”
in Conf. on Design and Architectures for Signal and Image Processing,
121
–127
(2010). Google Scholar
D. B. Heraset al.,
“Towards real-time hyperspectral image processing, a GP-GPU implementation of target identification,”
in IEEE 6th Int. Conf. on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS),
316
–321
(2011). Google Scholar
L. Santoset al.,
“Highly-parallel GPU architecture for lossy hyperspectral image compression,”
IEEE J. Sel. Topics Appl. Earth Observations Rem. Sens., 6
(2), 670
–681
(2013). http://dx.doi.org/10.1109/JSTARS.2013.2247975 1939-1404 Google Scholar
“CUDA technology,”
Nvidia Corporation,
(2013). http://www.nvidia.com/object/cuda_home_new.html Google Scholar
B. Hopsonet al.,
“Real-time CCSDS lossless adaptive hyperspectral image compression on parallel GPGPU amp; multicore processor systems,”
in NASA/ESA Conf. on Adaptive Hardware and Systems,
107
–114
(2012). Google Scholar
G. J. Sullivan,
“On embedded scalar quantization,”
in IEEE Int. Conf. on Acoustics, Speech, and Signal Processing,
iv-605
–iv-608
(2004). Google Scholar
J. Teuhola,
“A compression method for clustered bit-vectors,”
Inf. Process. Lett., 7
(6), 308
–311
(1978). http://dx.doi.org/10.1016/0020-0190(78)90024-8 IFPLAT 0020-0190 Google Scholar
M. HarrisM. Garland,
“Optimizing parallel prefix operations for the fermi architecture,”
GPU: Computing Gems Jade Edition, 29
–38 Morgan Kaufmann Pub, Boston
(2011). Google Scholar
A. Balevic,
“Parallel variable-length encoding on GPGPUs,”
in Proc. of Euro-Par09 Int. Conf. on Parallel Processing,
26
–35
(2009). Google Scholar
“Nvidia’s next generation CUDA compute architecture Fermi,”
Nvidia Corporation,
(2013). http://www.nvidia.com/content/PDF/fermi_white_papers/NVIDIAFermiComputeArchitectureWhitepaper.pdf Google Scholar
M. CiznickiK. KurowskiA. Plaza,
“GPU implementation of jpeg2000 for hyperspectral image compression,”
Proc. SPIE, 8183 81830H
(2011). http://dx.doi.org/10.1117/12.897386 PSISDG 0277-786X Google Scholar
BiographyLucana Santos received the telecommunication engineer degree by the University of Las Palmas de Gran Canaria in 2008, where she has been working towards the PhD degree at the Integrated Systems Design Division of the Institute for Applied Microelectronics (IUMA). In 2011 she was funded by the European Network of Excellence on High Performance and Embedded Architecture and Compilation (HiPEAC) to make research on architectures for hyperspectral image compression at the European Space Research and Technology Centre (ESTEC) in the Netherlands. Her research interests include hardware architectures for on-board data processing, video coding standards, and reconfigurable architectures. Enrico Magli received the PhD degree in electrical engineering in 2001, from Politecnico di Torino, Italy. He is currently an associate professor at the same university, where he leads the Image Processing Lab. His research interests include multimedia signal processing and networking, compressive sensing, distributed source coding, image and video security, and compression of satellite images. He is associate editor of the IEEE Transactions on Circuits and Systems for Video Technology, and of the EURASIP Journal on Information Security. He is a member of the Multimedia Signal Processing technical committee of the IEEE Signal Processing Society, and of the Multimedia Systems and Applications and the Visual Signal Processing and Communications technical committees of the IEEE Circuits and Systems Society. He has been coeditor of JPEG2000 Part 11—Wireless JPEG2000. He is general cochair of IEEE MMSP 2013, and has been TPC cochair of ICME2012, VCIP 2012, MMSP2011 and IMAP2007. He has published about 40 papers in refereed international journals, 3 book chapters, and over 90 conference papers. He is a corecipient of the IEEE Geoscience and Remote Sensing Society 2011 Transactions Prize Paper Award, and has received the 2010 Best Reviewer Award of IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing. He has received a 2010 Best Associate Editor Award of IEEE Transactions on Circuits and Systems for Video Technology. In 2011, he has been awarded from the European Union an ERC Starting Grant for a 5-year project titled "CRISP–Towards compressive information processing systems." Raffaele Vitulli received his MS degree in electronic engineering in 1991, from Politecnico of Bari, Italy. He is currently staff member of the European Space Agency, and he is working for the On-Board Payload Data Processing Section, located in ESTEC (NL). He is acting as main contact point for all the activities related to Satellite Data Compression in the Agency, and his interests are in the field of synthetic aperture radar, image and data compression, data handling, data processing, GPU and HW acceleration. He is participating to the work of the Consultative Committee for Space Data System, as a member of the Multispectral/Hyperspectral Data Compression Working Group. The mandate of the working group is the production of standards in the field of satellite data compression. He contributed to publish the CCSDS 122 Image Data Compression standard and the CCSDS 123 hyperspectral lossless compression standard. He is chairman and organizer of the On-Board Payload Data Compression Workshop. The workshop aims to bring together all the professionals working in the field of satellite data compression, to share the latest ideas and developments and to pave the way for the future technological challenges. The workshop, co-organized by ESA and CNES, is at the third edition and it is planned every two years. Antonio Nunez is full professor of electronic engineering at the University of Las Palmas GC, Spain. He has been dean of the Telecom Engineering School and is currently director of the Institute for Applied Microelectronics (IUMA) at ULPGC. He received the higher engineering degree in 1974 from the School of Telecommunication Engineering at the Technical University of Madrid UPM, and the PhD degree also from UPM in 1981. He was a research scientist with the Electrical Engineering Department of EPFL Lausanne, Switzerland, in 1981 and a visiting scientist (1986-1987) first at Stanford University and then at the School of Electrical Engineering of Purdue University, USA, where he continued as visiting professor the following year (1987–1988) working in specific high-speed digital signal processors. He has supervised 12 PhD theses. His current research fields include heterogeneous architecture platform based design and hardware-software codesign for embedded systems, system-level design of MPSoCs, multimedia processor architectures, hardware accelerators, and low-power optimization of integrated circuits, in particular for the application domains of real time image processing, video processing, video tracking and driver assistance systems in the automotive industry. He is a distinguished fellow of the International Society for Quality Electronic design ISQED, and a full member of HiPEAC, The European Network of Excellence in High Performance and Embedded Architecture and Compilation. He is also in the steering committees of ISQED, Euromicro DSD, PATMOS and DCIS. He is associate editor of several journals in the field. José F. López obtained the MS degree in physics (specialized in electronics) from the University of Seville, Spain, in 1989. In 1994, he obtained the PhD degree by the University of Las Palmas de Gran Canaria, Spain, and was awarded for his research in the field of high speed integrated circuits. He has conducted his investigations at the Research Institute for Applied Microelectronics (IUMA), where he is part of the Integrated Systems Design Division. He currently also lectures at the School of Telecommunication Engineering, in the University of Las Palmas de Gran Canaria (ULPGC), being responsible for the courses on VLSI circuits and digital circuits. He was with Thomson Composants Microondes (now United Monolithic Semiconductor, UMS), Orsay, France, in 1992. In 1995, he was with the Center for Broadband Telecommunications at the Technical University of Denmark (DTU), Lyngby, Denmark, and in 1996, 1997, 1999, and 2000 he was funded by the Edith Cowan University (ECU), Perth, Western Australia, to make research on low power, high performance integrated circuits and image processing. His main areas of interest are in the field of image and video processing, and VLSI circuits and systems. He has been actively enrolled in more than 15 research projects funded by the European Community, Spanish government and international private industries. He has written around 70 papers in national and international journals and conferences. Roberto Sarmiento received the MS and PhD degree in industrial engineering from the University of Las Palmas de Gran Canaria, Spain, in 1991. He is a full professor at the Telecommunication Engineering School at University of Las Palmas de Gran Canaria (ULPGC), Spain, in the area of electronic engineering. He contributed to set this school up, and he was the dean of the faculty from 1994 to 1995 and vice-chancellor for academic affairs and staff at the ULPGC from 1998 to 2003. In 1993, he was a visiting professor at the University of Adelaide, South Australia, and later at the University of Edith Cowan, also in Australia. He is a founder of the Research Institute for Applied Microelectronics (IUMA) and director of the Integrated Systems Design Division of this institute. Since 1990, he has published over 40 journal papers and book chapters and more than 120 conference papers. He has been awarded with three six-years research periods by the National Agency for the Research Activity Evaluation in Spain. He has participated in more than 35 projects and research programs funded by public and private organizations, from which he has been lead researcher in 15 of them, several funded by the European Union like GARDEN and the GRASS workgroup. He has got several agreements with companies for the design of high performance integrated circuits, where the most important are those performed with Vitesse Semiconductor Corporation, California. |
||||||||||||||||||||||||||||||||||||||||||||||||||||