|
|
1.IntroductionSpectral vegetation indices (VIs) have been used as proxies to such biophysical parameters as leaf area index (LAI), fraction of absorbed photosynthetically active radiation, and gross primary productivity (e.g., Ref. 1). The normalized difference vegetation index (NDVI), which is the difference between the near-infrared (NIR) and red reflectances divided by their sum, has been the most widely used index in regional to global studies of terrestrial vegetation. In particular, the NDVI time series from the National Oceanic and Atmospheric Administration’s (NOAA) advanced very-high-resolution radiometer (AVHRR) sensor series has extensively been used in studies involving climate–vegetation interactions.2,3 The enhanced vegetation index (EVI), an index developed for moderate-resolution imaging spectroradiometer (MODIS) of the National Aeronautics and Space Administration’s (NASA) Earth Observing System (EOS), has also been applied successfully to various vegetation studies, including land surface phenology,4 ecosystem modeling,5,6 and evapotranspiration estimation.7 The EVI was designed to optimize the vegetation signal with improved sensitivity in high biomass regions and improved vegetation monitoring through a decoupling of the canopy background signal and a reduction in atmospheric aerosol influences,8 and complements the NDVI. where are the total- or partial (uncorrected for aerosols)-atmosphere corrected reflectances, , , and indicate the NIR, red, and blue bandpasses, respectively, is the canopy background adjustment factor, and and are the coefficients of the aerosol resistance term. The coefficients adopted in the MODIS EVI algorithm are , , , .9A new EVI data record has begun to be collected with the visible infrared imaging radiometer suite (VIIRS) sensor series.10 The first VIIRS sensor onboard the Suomi National Polar-Orbiting Partnership (NPP) platform was successfully launched in October 2011. VIIRS is slated to replace the NOAA AVHRR sensor series and to continue the highly calibrated data stream begun with EOS-MODIS. VIIRS incorporates many of the technological advancements developed for EOS-MODIS, and a number of geophysical products, termed environmental data records, are produced from VIIRS data, including the NDVI, albedo, and land surface temperature in addition to the EVI.11 It is vital to evaluate multisensor compatibility of satellite-derived products.12–15 Differences in both sensor and/or platform characteristics (e.g., spatial resolution, spectral bandpass, and sun-target-view geometry)16–20 and product generation algorithms (e.g., atmospheric correction)21 can lead to systematic differences in multisensor products. The spectral bandpass is one such sensor characteristic that varies across sensors, requiring investigations, in particular, for multisensor VI and reflectance compatibility.22–25 Figure 1 compares, for example, the VIIRS and MODIS spectral response curves for the blue, red, and NIR bands (available at http://mcst.gsfc.nasa.gov/calibration/parameters and http://www.star.nesdis.noaa.gov/jpss/VIIRS.php for MODIS and VIIRS, respectively). The smallest difference is observed for the NIR bands where the VIIRS band covers slightly longer wavelengths than the MODIS counterpart. The largest difference is observed for the VIIRS and MODIS blue bands that are positioned at two disparate wavelength regions while having the same bandwidth. The VIIRS red bandpass is wider than that of MODIS, but encompasses the MODIS red band entirely. Fig. 1Normalized spectral response curves of visible infrared imaging radiometer suite (VIIRS) and moderate-resolution imaging spectroradiometer (MODIS) bands: blue (VIIRS-M3 and MODIS-3), red (VIIRS-I1 and MODIS-1), and near-infrared (VIIRS-I2 and MODIS-2). 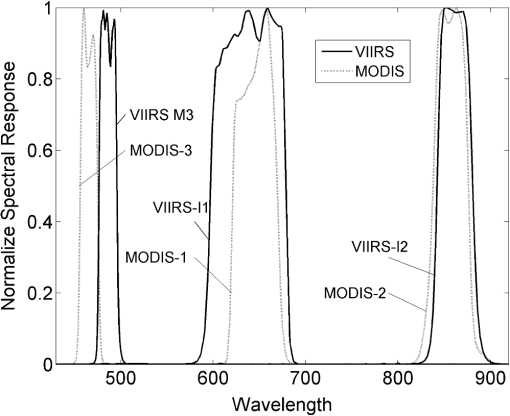 Several studies have empirically examined the impact of spectral bandpass differences on cross-sensor EVI compatibility.12,26,27 In their spectral simulation analysis with a set of Hyperion scenes acquired along a tropical forest-savanna ecological gradient in Brazil, Kim et al.27 found that VIIRS EVI values were larger than MODIS EVI mainly due to their disparate blue bands, with the maximum difference reaching 0.040 EVI units. Miura and Yoshioka26 also found the same trend in their Hyperion-based bandpass simulation analysis performed over five AERONET sites in the conterminous United States. Fensholt et al.12 analyzed field measured spectral data at a savanna site in Senegal and found that MODIS EVI was higher than the Satellite Pour 1’Observation de la Terre (SPOT)-VEGETATION counterpart with the slope and offset of a MODIS versus VEGETATION regression line being 1.33 and 0.08. Fensholt et al.12 also found a reduced consistency between the EVI from these two sensors compared to the NDVI due to the different atmospheric correction schemes of the blue band used in the two sensors, indicating the importance of accurately correcting molecular scattering and absorption effects for the EVI. In contrast to the EVI, a large number of studies have addressed the effects of spectral bandpass differences on multisensor NDVI compatibility, many of which have resulted in proposing spectral transformation methods (e.g., Refs. 28, 29, and 30). A majority of these studies derived first- or higher-order polynomials that spectrally calibrated the NDVI of one sensor to that of another.28,30–34 This empirical VI-to-VI translation approach has been found effective in reducing systematic differences among multisensor NDVIs. Other studies weight-averaged several narrow bands of one sensor to simulate a broader band of another sensor where the optimum weight(s) was determined to provide the best NDVI compatibility between the two sensors.35–37 This band-averaging approach has only been proposed for MODIS-to-AVHRR,35,36 and medium-resolution imaging spectrometer (MERIS)-to-AVHRR NDVI translations.37 These studies have shown that MODIS and MERIS NDVIs can be made spectrally compatible to AVHRR NDVI. Gao,36 for example, performed a bandpass simulation analysis using AVIRIS data acquired in Florida and Nevada and demonstrated a 90% reduction in the mean difference between AVHRR NDVI and an AVHRR-compatible NDVI derived with four MODIS bands. Weighted averaging, however, may degrade the enhanced capability of narrow bands by, for example, recontaminating the data with atmospheric water vapor.36 Likewise, the methodology is only applicable to certain pairs of sensors. Another set of studies derived cross-sensor spectral transformation equations analytically using vegetation isoline equations.38,39 Vegetation isoline equations relate two spectral reflectances at two different wavelengths based on the radiative transfer through the atmosphere-canopy-soil system.40 This isoline-based approach was used to translate MODIS red and NIR reflectances to the counterparts of Landsat-7 enhanced Thematic Mapper plus (ETM+) and NOAA-14 AVHRR, which resulted in reductions in mean NDVI differences for those sensor pairs.38 The approach was also used to theoretically investigate intersensor relationships of two-band VIs,39 including the NDVI, soil-adjusted vegetation index,41 and two-band EVI (EVI2).42 Yoshioka et al.39 found that the two-band VI translation equation was a rational function of the source sensor VI where the coefficients of the equation were a function of soil, canopy, and atmosphere. In this study, we used vegetation isoline equations and derived a cross-sensor spectral transformation equation for the three-band EVI for MODIS to VIIRS continuity/compatibility. First, the isoline equations were used to obtain band-to-band translation equations from the VIIRS red, NIR, and blue to the MODIS respective counterparts. We then substituted the derived translation equations for the MODIS reflectances in the EVI equation [Eq. (1)], thus formulating a MODIS-compatible VIIRS EVI. In the reminder of this paper, we first describe the derivation along with a brief review of vegetation isoline equations in Sec. 2. The derived MODIS-compatible EVI is then evaluated for accuracy and characterized for sensitivity by a numerical experiment in Secs. 3 and 4. Finally, we present results of the calibration exercises through comparisons of model-simulated and actual sensor data, and examine the practical utility of our translation derivations in Sec. 5. 2.Derivation of MODIS-Compatible VIIRS EVIWhen vegetation canopy spectra are cross-plotted at two wavelengths (e.g., red-NIR reflectance plots), those spectra over a constant canopy and atmosphere [e.g., any constant leaf area index (LAI) and aerosol optical thickness (AOT), respectively] with varying underlying backgrounds can be represented by a line connecting these various background-dependent spectra with a slope and offset specific to those values of LAI and AOT (Ref. 43). These lines are known as vegetation isolines.41 Vegetation isoline equations analytically represent the vegetation isolines.40 Details of and assumptions used in the derivation of the equations are found elsewhere (e.g., Refs. 44 and 45); here we provide a brief review. The derivation assumes a horizontally infinite homogeneous atmospheric layer.40,44,45 The target surface is assumed to consist of vegetation and bare soil, where the radiative transfer problem in the vegetation-covered and uncovered areas can be simulated independently by modeling a horizontally infinite homogeneous canopy and bare soil, respectively. Under these assumptions, the top-of-atmosphere (TOA) reflectance, , and the reflectance of the surface target, or top-of-canopy (TOC) reflectance, , which is a linear weighted sum of vegetation and soil spectra with a fraction of green vegetation cover, is represented as follows: where is the fraction of green vegetation cover (vertically projected area), is the two-way atmospheric transmittance due to molecular and aerosol scattering, is the two-way transmittance of vegetation layer, is the intrinsic atmospheric reflectance due to molecular and aerosol scattering, is the intrinsic reflectance of vegetation layer, is the spherical albedo of atmospheric layer, is the spherical albedo of vegetation layer, and is the reflectance of soil surface. For brevity, we omit the sun and view angles from Eqs. (2) and (3).Let two sensors of interest be sensor-1 and sensor-2. The TOA reflectance of sensor-1 at the wavelength [Eqs. (2) and (3) for ] and that of sensor-2 at the wavelength [Eqs. (2) and (3) for ] can be related using the relationship for the soil layer, known as the soil line.46 The linear relationship between any two bands for soil reflectances were assumed as where the two parameters and are the slope and offset of the soil line, respectively. After truncating the higher-order interaction terms between the atmosphere and vegetation layers [Eq. (2)] and between the vegetation and soil background layers [Eq. (3)] for and , and are eliminated using Eq. (4), which derives the vegetation isoline equations.40 whereThe slope and offset of the vegetation isoline equation [ and , respectively] are a function of atmosphere (e.g., AOT) and vegetation biophysical (e.g., LAI) conditions, but independent of canopy background brightness. Errors due to the truncation of the higher-order terms are reported minimal, but larger for brighter soil backgrounds.40 In MODIS and VIIRS products, the input reflectances for the EVI computations are TOC reflectances, or corrected for total atmospheric effects, including molecular scattering, gaseous absorptions, and aerosol effects. Partial atmosphere corrected (PAC) reflectances (uncorrected for aerosols) can also be used to compute the EVI.8 In this study, both the TOC and PAC reflectances were considered, and PAC reflectances were modeled by adding the aerosol layer over the canopy. Below, the atmospheric parameters of and within the isoline parameters [Eqs. (7), (10), and (11)] describe the reflectance and transmittance of the aerosol layer. and are zero and unity, respectively, for TOC reflectances. Let sensor-1 and sensor-2 be VIIRS (the source sensor) and MODIS (the target sensor), respectively. Then, the EVI for MODIS, , is of the form Vegetation isoline equations can be used to relate the NIR, red, and blue reflectances of VIIRS, , , and , to the corresponding MODIS reflectances. The MODIS-compatible VIIRS EVI, , can be derived by substituting Eqs. (13), (14), and (15) for , , and in Eq. (12), respectively. whereEquation (16) has four new coefficients, all of which are a function of vegetation isoline parameters and one of which also contains the EVI coefficients (, , and ). This indicates that the bias magnitude between the two EVIs changes with the soil, vegetation, and aerosol conditions and that the exact translation is possible only when these conditions are known. The four coefficients, , , , and , become 1, 0, 1, and , respectively, when the bandpasses of the two sensors are identical. The derived MODIS-like EVI [Eq. (16)] should also be subject to errors due to the assumptions used in the derivation of the vegetation isoline equation described above.40 3.Performance Evaluation with Numerical ExperimentA numerical experiment was conducted to evaluate the performance of the derived EVI [Eq. (16)]. The PROSAIL canopy reflectance model47–49 and the 6S atmospheric radiative transfer model50 were employed to simulate TOC and PAC reflectances of the VIIRS and MODIS spectral bands for a range of vegetation and atmosphere conditions. Table 1 summarizes the input parameter values and ranges used in the simulation. Table 1Input parameter values used in reflectance simulations.
Soil reflectance spectra [ in Eq. (3)] from a 2002 MODIS field campaign in Brazil51 were obtained. These spectra were collected using an ASD FieldSpec Pro FR (Analytical Spectral Devices Inc., Boulder, Colorado). There were 35 spectra (400 to 2500 nm at 1 nm resolution) of soils from Brasilia, Araguaia, and Tapajos, from which a mean and standard deviation (std.) were computed for every wavelength. Using these statistics, we produced five soil spectra of varying brightness (i.e., mean, , and ) for the use in canopy reflectance modeling where the soil layer was assumed as a Lambertian surface. TOC reflectances were obtained using Eq. (3) where reflectances over the vegetated area were obtained using PROSAIL. As described in the previous section, we considered TOC reflectances as total atmosphere corrected reflectances and assumed an aerosol atmosphere to simulate PAC reflectances. Reflectances, transmittances, and spherical albedos of the aerosol atmosphere computed with the 6S (, , and ) were added to the TOC reflectances using Eq. (2). All simulations were performed at 1 nm spectral resolution. The simulated reflectance spectra were spectrally convolved to VIIRS and MODIS bandpass reflectances using their respective spectral response curves. Vegetation isoline parameters were also extracted from these model simulations. First, and obtained by 6S were spectrally convolved and used as isoline parameter values. Second, soil line slopes and offsets [ and in Eq. (4)] were obtained by regressing VIIRS reflectances to MODIS reflectances which were obtained by convolving the five soil spectra to MODIS and VIIRS bandpasses (blue, red, or NIR). The soil line slopes for VIIRS-MODIS blue, red, and NIR bands were 0.94, 1.02, and 1.00, respectively, with offsets of , 0.001, and , respectively (the coefficients of determination for three bands were 0.995, 0.999, and 0.999, respectively). Last, two-way canopy transmittances () were obtained by solving for of Eq. (3) when is equal to unity and is approximated by (Ref. 44) as shown in Eq. (21). The canopy reflectance simulated without a soil background (a perfect absorber), which is in Eq. (3), and the canopy reflectance simulated over an arbitrary soil background reflectance () of 0.14 at 850 nm, , were computed using PROSAIL. MODIS EVI () and VIIRS EVI () [Eq. (1)] were computed from the simulated reflectances. The MODIS-compatible EVI was derived by using VIIRS TOC/PAC reflectances and the isoline parameters in Eq. (16). minus () and minus () were used to evaluate the MODIS-compatible VIIRS EVI derivation. Root mean square errors (RMSE) of with respect to and were also computed. where is ’th sample of , is ’th sample of either or , and is the sample size, which was equal to 46,305 in this numerical experiment.and are plotted against in Fig. 2. ranged from to 0.009 with a trend that changed from negative to positive values with increasing EVI values. was much smaller than with its magnitude EVI units. Residual errors were attributed to the first-order approximation of vegetation isoline equations. The isoline equations truncated the higher-order terms (multiple scattering) between atmosphere and vegetation and between vegetation and soil surface. But the magnitude of the residual errors () was considered insignificant. Fig. 2MODIS enhanced vegetation index (EVI) minus VIIRS EVI () and MODIS EVI minus MODIS-compatible VIIRS EVI () plotted against MODIS EVI (). 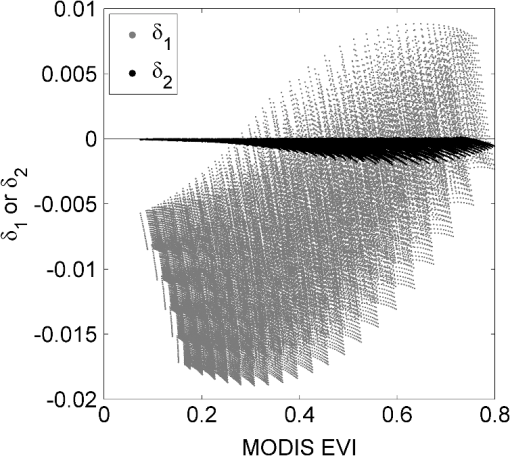 RMSE between and , and between and were 0.01 and 0.0004 EVI units, respectively, the latter being less than one order of magnitude of the former. The results indicated that the isoline-based translation equation of the EVI [Eq. (16)] performed well for VIIRS to MODIS. 4.Sensitivity AnalysisAs seen in Sec. 2, the parameters are a function of vegetation and atmosphere [see Eqs. (17) to (20)]. In other words, vary with vegetation and atmosphere conditions. Using the same modeling conditions as in the previous section, sensitivities to AOT, total LAI, and fractional vegetation cover (FVC) were evaluated in this section (Fig. 3). Fig. 3Contour plots of (, 2, 3, and 4) as a function of aerosol optical thickness (AOT) and total leaf area index (total LAI) for three fractional vegetation cover (FVC) values. The top four plots [(a) to (d)] are for , the middle four [(e) to (h)] for , and the bottom four [(i) to (l)] for . The contour intervals for , , , and are 0.002, 0.0002, 0.01, and 0.01, respectively. 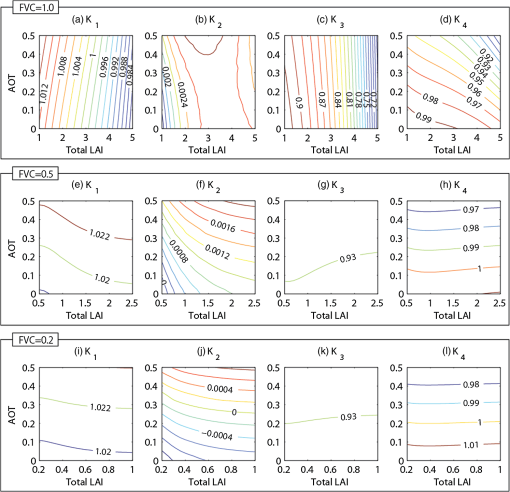 Figures 3(a) to 3(c) show that , , and were basically a function of total LAI for a full-vegetation-covered target. Only was sensitive to both AOT and total LAI [Fig. 3(d)]. When the vegetation cover decreased to 50%, to became somewhat sensitive to both AOT and total LAI [Figs. 3(e) to 3(g)], whereas became sensitive only to AOT [Fig. 3(h)]. At FVC of 0.2, all values were primarily a function of AOT [Figs. 3(i) to 3(l)]. With a decrease in FVC, variability in was largely reduced. varied from 0.980 to 1.016 (0.036 difference) at 1.0 FVC [Fig. 3(a)] and varied from 1.019 to 1.024 (0.005 difference) at 0.2 FVC [Fig. 3(i)]. Similarly, variability in was dramatically reduced with its range from 0.695 to 0.917 (0.222 difference) at 1.0 FVC [Fig. 3(c)] and from 0.923 to 0.935 (0.012 difference) at 0.2 FVC [Fig. 3(k)]. At any given values of total LAI and AOT, , , and values decreased with increasing FVC values (Fig. 3). The maximum and minimum values found in this simulation are summarized in Table 2. Table 2Maxima and minima of Ki resulted from the simulation.
In summary, the sensitivities of to total LAI and AOT varied with FVC and were higher when FVC were close to the full cover. At higher FVC (), total LAI was the main factor to influence except . AOT had a greater influence on than total LAI when the surface was partially covered with vegetation. 5.Optimization5.1.Optimization AlgorithmAs a first practical application of the derived equations, we considered finding a single set of values that minimizes differences between the MODIS-compatible VIIRS EVI and the MODIS EVI via regression and determines whether that single set of values could provide a reasonable level of compatibility. The simulation dataset from Sec. 3, and actual MODIS and VIIRS surface reflectance data were used in this evaluation. From the practical point of view, it is not reasonable to estimate values for every single spectrum for intersensor EVI translation as that requires rigorous computations, for example, inverting radiative transfer models to obtain physical variables, including AOT, LAI, chlorophyll contents, and background soil optical properties. Since the MODIS-compatible EVI is nonlinear in [Eq. (16)], the optimization problem here would contain multiple local minima. In this case, the derivatives would not necessarily provide an appropriate direction to search for the optimal solution. We therefore employed the Nelder-Mead simplex method “fminsearch” in Optimization Toolbox of MATLAB® R2012b (MathWorks Inc., Natick, Massachusetts) to search for the global minimum without derivatives, but with multiple initial guesses. The mean absolute difference (MAD) between and was used as the merit function. This optimization algorithm was started with 100 sets of randomly distributed initial values and that set of values which resulted in the smallest merit function value [Eq. (23)], , was selected as the optimum solution. The difference between and MODIS-like VIIRS EVI with , , was then evaluated. 5.2.Optimization with Simulated DataThe simulation dataset from Sec. 3 consisted of 46,305 pairs of simulated MODIS and VIIRS reflectance spectra. Parameter values obtained through the optimization reduced systematic errors between MODIS-compatible VIIRS EVI and MODIS EVI successfully (Fig. 4). The resultant parameter values were . The mean of and were and 0.0001. Variability of was much smaller than that of (RMSE changed from 0.01 to 0.0017; an 83% reduction), although not as small as that of (0.0004, see Sec. 3). Fig. 4MODIS EVI minus VIIRS EVI () and MODIS-compatible VIIRS EVI using optimized parameters minus MODIS EVI () plotted against MODIS EVI () for simulated data. 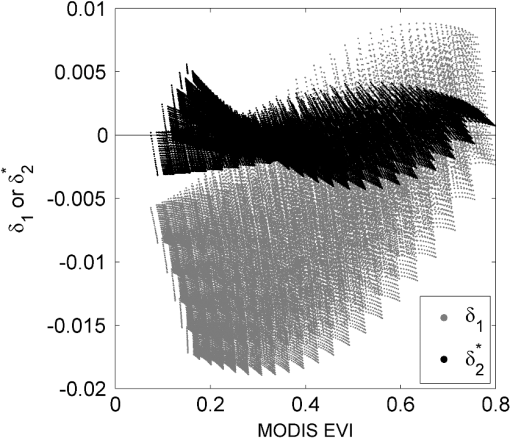 The optimal parameter values were all outside the ranges of found in Sec. 4 (Table 2). , for example, was 1.131 whereas the maximum value of was 0.935. These optimal parameter values were obtained by merely and specifically minimizing the merit function on the simulated spectral dataset. In other words, this was a regression problem and, thus, the optimal parameter values could be found outside the ranges found in the physical computations in Sec. 4. Variability of differences between the MODIS-compatible VIIRS EVI and MODIS EVI was 83% smaller than that between VIIRS EVI and MODIS EVI. This is because if the structure of the merit function over parameter space (i.e., MAD over the reflectance space) is suitable for the function to be fit (i.e., MODIS-compatible EVI with optimum parameters, ), the optimization would work well (variability would decrease). 5.3.Optimization with Actual DataVIIRS and MODIS data over North America on August 2013 were obtained for testing the optimization with actual sensor data. Pairs of Aqua MODIS and VIIRS atmospherically corrected reflectance spectra on the same date at the same coordinates were extracted. The pairs were restricted to near-nadir viewing (0 to 5 view zenith angles). Since AquaMODIS and Suomi NPP VIIRS both have a 1:30 p.m. equator crossing time, their spectral measurement times were close to each other where solar zenith angle differences were to 2 deg. The day of years (DOYs), 223 and 239 (August 11 and 27, respectively) were selected as with near-nadir view were available for the days. Aqua MODIS bands 1 to 3 surface reflectances (L2G daily 500 m, Collection 5) were aggregated to generate 1-km-resolution data. The state quality assurance with 1-km resolution was used to screen the data (Table 3). Suomi NPP VIIRS L2G daily 500-m surface reflectance product was used to obtain VIIRS-I1 and VIIRS-I2 data and the corresponding 1-km product was acquired for VIIRS-M3 data, which are a VIIRS Land Product Evaluation and Analysis Tool Element (Land PEATE) Archive Set 3002 [products generated by the Land PEATE using NASA Land Science Team Adjusted version of the NOAA’s near-real-time Interface Data Processing Segment software].52 These data were generated by gridding 375- and 750-m resolution swath data into 500-m and 1-km grids, respectively. Impacts of the errors associated with gridding and coarsening spatial resolution are not discussed here. I1 and I2 data were aggregated to 1-km resolution. The land quality flags in the 1-km-resolution data were used to screen VIIRS data (Table 3). The product generation algorithm (e.g., atmospheric correction) for VIIRS surface reflectance had still been under intensive validation and calibration, and was not identical to that of MODIS, inducing/increasing random and systematic errors between MODIS and VIIRS EVI. A total number of pairs of 1-km MODIS and VIIRS reflectance spectra, which satisfied the conditions (near-nadir view in specific DOYs), was 51,188. Table 3Moderate-resolution imaging spectroradiometer (MODIS) state quality assurance (QA) and visible infrared imaging radiometer suite (VIIRS) land quality flags used in the optimization.
MODIS EVI minus VIIRS EVI () computed using the sample data is shown in a density plot ( versus ) in Fig. 5(a). There was a peak in MODIS EVI around 0.2, and many samples fell between 0.1 and 0.6 in MODIS EVI units. The mean of and its variability (RMSE) were and 0.039. MODIS EVI minus MODIS-compatible VIIRS EVI obtained via the optimization () were plotted against MODIS EVI ( versus ) in Fig. 5(b). The mean of and its variability were 0.001 and 0.023. Variability of was reduced from those of (RMSE changed from 0.039 to 0.023; a 41% reduction). Fig. 5Density plot of EVI differences against MODIS EVI with actual MODIS and VIIRS data. (a) MODIS EVI minus VIIRS EVI () against MODIS EVI (). (b) MODIS EVI minus MODIS-compatible VIIRS EVI using optimized parameters () against MODIS EVI (). Ranges of axis for the density plots were 0.1. 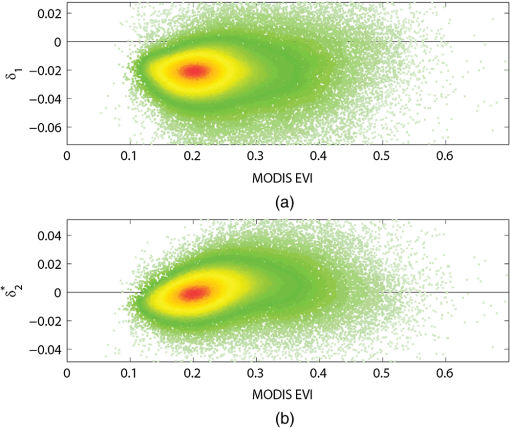 A set of parameter values obtained via the optimization was , which was different from the one for the simulated data []. This was attributed to several factors including a gap between modeled and real data, differences in conditions/land cover of samples. Note that limited conditions were imposed to extract the sample data for this calibration exercise; hence, the optimum values, , for other regions/global data with different time periods likely result in slightly different values. The RMSE reduction with the MODIS-compatible EVI for actual data (41%) was lower than a half of that obtained with the simulated data (83%). The variability in the original EVI differences of actual data, , were caused not only by systematic errors due to bandpass differences but also by geolocation errors, algorithm differences (atmospheric correction and quality flags), radiometric calibration uncertainty, and other factors. This likely limited the reduction in variability in . 6.Summary and DiscussionA cross-sensor spectral transformation equation for the three-band EVI was derived based on vegetation isoline equations, aimed at intersensor EVI continuity/compatibility between MODIS and VIIRS. The derived equation contained four parameters that changed with soil, vegetation, and atmospheric conditions. Our performance evaluation verified the derivation where residual errors caused by the truncation of higher-order terms of vegetation isoline equations were acceptable. The sensitivity analysis showed that total LAI and AOT were mainly responsible for variations of the coefficients at higher and lower FVC values, respectively. A set of fixed coefficient values found with an optimization technique successfully reduced differences between the spectrally transformed MODIS-compatible VIIRS EVI and the MODIS EVI for both model-simulated and actual sensor data. The derivations introduced in this study have no limitation with respect to sensors as long as they measure the blue, red, and NIR wavelength regions. Therefore, the same methodology can be applied not only to MODIS and VIIRS, but also to other existing and future sensors, including SPOT VEGETATION, Environmental Satellite (ENVISAT) MERIS, Sentinel-3, and Global Change Observation Mission-Climate (GCOM-C) Global Imager (GLI), for data continuity/compatibility across multiagency and/or international collaboration. The derivation should also be useful for examining multiresolution spectral compatibility of the three-band EVI involving MODIS/VIIRS and the Landsat sensor series (i.e., TM, ETM+, and Operational Land Imager), while this would require a separate study on spatial compatibility of the EVI across different spatial resolution data. The numerical simulations used for the accuracy assessment, sensitivity analysis, and calibration exercise had a limited range of atmosphere, canopy, and soil conditions and were for a standard sun-target-sensor geometry (i.e., near-nadir and moderate sun angle). Additional studies that involve model simulations with a wider range of conditions and actual image data analyses with broader spatial and temporal coverage should be conducted to further characterize and evaluate the derived translation equation. In particular, analyses of global VIIRS and MODIS data will be required to obtain reliable optimization results. AcknowledgmentsThis work was supported by a NASA NPP grant NNX11AH25G (T.M.), a NOAA contract (T.M.), and a JSPS KAKENHI 21510019 (H.Y.). ReferencesE. P. Glennet al.,
“Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: what vegetation indices can and cannot tell us about the landscape,”
Sensors, 8
(4), 2136
–2160
(2008). http://dx.doi.org/10.3390/s8042136 SNSRES 0746-9462 Google Scholar
L. Bounouaet al.,
“Sensitivity of climate to changes in NDVI,”
J. Climate, 13
(13), 2277
–2292
(2000). http://dx.doi.org/10.1175/1520-0442(2000)013<2277:SOCTCI>2.0.CO;2 JLCLEL 0894-8755 Google Scholar
R. de Jonget al.,
“Analysis of monotonic greening and browning trends from global NDVI time-series,”
Remote Sens. Eviron., 115
(2), 692
–702
(2011). http://dx.doi.org/10.1016/j.rse.2010.10.011 RSEEA7 0034-4257 Google Scholar
S. Gangulyet al.,
“Land surface phenology from MODIS: characterization of the Collection 5 global land cover dynamics product,”
Remote Sens. Environ., 114
(8), 1805
–1816
(2010). http://dx.doi.org/10.1016/j.rse.2010.04.005 RSEEA7 0034-4257 Google Scholar
R. B. Gurunget al.,
“Predicting enhanced vegetation index (EVI) curves for ecosystem modeling applications,”
Remote Sens. Environ., 113
(10), 2186
–2193
(2009). http://dx.doi.org/10.1016/j.rse.2009.05.015 RSEEA7 0034-4257 Google Scholar
X. Xiaoet al.,
“Satellite-based modeling of gross primary production in an evergreen needleleaf forest,”
Remote Sens. Environ., 89
(4), 519
–534
(2004). http://dx.doi.org/10.1016/j.rse.2003.11.008 RSEEA7 0034-4257 Google Scholar
P. L. Nagleret al.,
“Evapotranspiration on western U.S. rivers estimated using the enhanced vegetation index from MODIS and data from eddy covariance and Bowen ratio flux towers,”
Remote Sens. Environ., 97
(3), 337
–351
(2005). http://dx.doi.org/10.1016/j.rse.2005.05.011 RSEEA7 0034-4257 Google Scholar
A. R. Hueteet al.,
“Overview of the radiometric and biophysical performance of the MODIS vegetation indices,”
Remote Sens. Environ., 83
(1–2), 195
–213
(2002). http://dx.doi.org/10.1016/S0034-4257(02)00096-2 RSEEA7 0034-4257 Google Scholar
A. R. HueteC. O. JusticeH. Q. Liu,
“Development of vegetation and soil indices for MODIS-EOS,”
Remote Sens. Environ., 49
(3), 224
–234
(1994). http://dx.doi.org/10.1016/0034-4257(94)90018-3 RSEEA7 0034-4257 Google Scholar
“Committee on Earth Science and Applications from Space: A Community Assessment and Strategy for the Future, National Research Council,”
Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond, The National Academies Press, Washington, D.C.
(2007). Google Scholar
R. L. VogelJ. L. PrivetteY. Yu,
“Creating proxy VIIRS data from MODIS: spectral transformations for mid- and thermal-infrared bands,”
IEEE Trans. Geosci. Remote Sens., 46
(11), 3768
–3782
(2008). http://dx.doi.org/10.1109/TGRS.2008.923320 IGRSD2 0196-2892 Google Scholar
R. FensholtI. SandholtS. Stisen,
“Evaluating MODIS, MERIS, and VEGETATION vegetation indices using in situ measurements in a semiarid environment,”
IEEE Trans. Geosci. Remote Sens., 44
(7), 1774
–1786
(2006). http://dx.doi.org/10.1109/TGRS.2006.875940 IGRSD2 0196-2892 Google Scholar
O. SamainB. GeigerJ. L. Roujean,
“Spectral normalization and fusion of optical sensors for the retrieval of BRDF and albedo: application to VEGETATION, MODIS, and MERIS data sets,”
IEEE Trans. Geosci. Remote Sens., 44
(11), 3166
–3179
(2006). http://dx.doi.org/10.1109/TGRS.2006.879545 IGRSD2 0196-2892 Google Scholar
M. Schmidtet al.,
“Long term data fusion for a dense time series analysis with MODIS and Landsat imagery in an Australian savanna,”
J. Appl. Remote Sens., 6 063512
(2012). http://dx.doi.org/10.1117/1.JRS.6.063512 1931-3195 Google Scholar
T. MiuraA. R. HueteH. Yoshioka,
“An empirical investigation of cross-sensor relationships of NDVI and red/near-infrared reflectance using EO-1 Hyperion data,”
Remote Sens. Environ., 100
(2), 223
–236
(2006). http://dx.doi.org/10.1016/j.rse.2005.10.010 RSEEA7 0034-4257 Google Scholar
A. H. StrahlerC. E. WoodcockJ. Smith,
“On the nature of models in remote sensing,”
Remote Sens. Environ., 20
(2), 121
–139
(1986). http://dx.doi.org/10.1016/0034-4257(86)90018-0 RSEEA7 0034-4257 Google Scholar
C. O. Justiceet al.,
“Spatial degradation of satellite data,”
Int. J. Remote Sens., 10
(9), 1539
–1561
(1989). http://dx.doi.org/10.1080/01431168908903989 IJSEDK 0143-1161 Google Scholar
J. N. EpiphanioA. R. Huete,
“Dependence of NDVI and SAVI on Sun/sensor geometry and its effect on fAPAR relationships in Alfalfa,”
Remote Sens. Environ., 51
(3), 351
–360
(1995). http://dx.doi.org/10.1016/0034-4257(94)00110-9 RSEEA7 0034-4257 Google Scholar
J. Verrelstet al.,
“Angular sensitivity analysis of vegetation indices derived from CHRIS/PROBA data,”
Remote Sens. Environ., 112
(5), 2341
–2353
(2008). http://dx.doi.org/10.1016/j.rse.2007.11.001 RSEEA7 0034-4257 Google Scholar
H. WuZ.-L. Li,
“Scale issues in remote sensing: a review on analysis, processing and modeling,”
Sensors, 9
(3), 1768
–1793
(2009). http://dx.doi.org/10.3390/s90301768 SNSRES 0746-9462 Google Scholar
T. MiuraJ. P. TurnerA. R. Huete,
“Spectral compatibility of the NDVI across VIIRS, MODIS, and AVHRR: an analysis of atmospheric effects using EO-1 Hyperion,”
IEEE Trans. Geosci. Remote Sens., 51
(3), 1349
–1359
(2013). http://dx.doi.org/10.1109/TGRS.2012.2224118 IGRSD2 0196-2892 Google Scholar
C. D. ElvidgeZ. Chen,
“Comparison of broad-band and narrow-band red and near-infrared vegetation indices,”
Remote Sens. Environ., 54
(1), 38
–48
(1995). http://dx.doi.org/10.1016/0034-4257(95)00132-K RSEEA7 0034-4257 Google Scholar
R. Bryantet al.,
“Data continuity of Earth Observing 1 (EO-1) Advanced Land I Satellite Imager (ALI) and Landsat TM and ETM+,”
IEEE Trans. Geosci. Remote Sens., 41
(6), 1204
–1214
(2003). http://dx.doi.org/10.1109/TGRS.2003.813213 IGRSD2 0196-2892 Google Scholar
P. M. Teilletet al.,
“Impacts of spectral band difference effects on radiometric cross-calibration between satellite sensors in the solar-reflective spectral domain,”
Remote Sens. Environ., 110
(3), 393
–409
(2007). http://dx.doi.org/10.1016/j.rse.2007.03.003 RSEEA7 0034-4257 Google Scholar
E. SwinnenF. Veroustraete,
“Extending the SPOT-VEGETATION NDVI time series (1998–2006) back in time with NOAA-AVHRR data (1985-1998) for Southern Africa,”
IEEE Trans. Geosci. Remote Sens., 46
(2), 558
–572
(2008). http://dx.doi.org/10.1109/TGRS.2007.909948 IGRSD2 0196-2892 Google Scholar
T. MiuraH. Yoshioka,
“Hyperspectral data in long-term, cross-sensor continuity studies,”
Hyperspectral Remote Sensing of Vegetation, 607
–627 CRC Press, Boca Raton, Florida
(2011). Google Scholar
Y. Kimet al.,
“Spectral compatibility of vegetation indices across sensors: band decomposition analysis with Hyperion data,”
J. Appl. Remote Sens., 4 043520
(2010). http://dx.doi.org/10.1117/1.3400635 1931-3195 Google Scholar
M. D. Stevenet al.,
“Intercalibration of vegetation indices from different sensor systems,”
Remote Sens. Environ., 88
(4), 412
–422
(2003). http://dx.doi.org/10.1016/j.rse.2003.08.010 RSEEA7 0034-4257 Google Scholar
L. Jiet al.,
“Agreement evaluation of AVHRR and MODIS 16-day composite NDVI data sets,”
Int. J. Remote Sens., 29
(16), 4839
–4861
(2008). http://dx.doi.org/10.1080/01431160801927194 IJSEDK 0143-1161 Google Scholar
A. P. TrishchenkoJ. CihlarZ. Li,
“Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors,”
Remote Sens. Environ., 81
(1), 1
–18
(2002). http://dx.doi.org/10.1016/S0034-4257(01)00328-5 RSEEA7 0034-4257 Google Scholar
A. P. Trishchenko,
“Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: extension to AVHRR NOAA-17, 18 and METOP-A,”
Remote Sens. Environ., 113
(2), 335
–341
(2009). http://dx.doi.org/10.1016/j.rse.2008.10.002 RSEEA7 0034-4257 Google Scholar
W. J. D. van Leeuwenet al.,
“Multi-sensor NDVI data continuity: uncertainties and implications for vegetation monitoring applications,”
Remote Sens. Environ., 100
(1), 67
–81
(2006). http://dx.doi.org/10.1016/j.rse.2005.10.002 RSEEA7 0034-4257 Google Scholar
P. D’Odoricoet al.,
“Experimental evaluation of Sentinel-2 spectral response functions for NDVI time-series continuity,”
IEEE Trans. Geosci. Remote Sens., 51
(3), 1336
–1348
(2013). http://dx.doi.org/10.1109/TGRS.2012.2235447 IGRSD2 0196-2892 Google Scholar
A. GonsamoJ. M. Chen,
“Spectral response function comparability among 21 satellite sensors for vegetation monitoring,”
IEEE Trans. Geosci. Remote Sens., 51
(3), 1319
–1335
(2013). http://dx.doi.org/10.1109/TGRS.2012.2198828 IGRSD2 0196-2892 Google Scholar
A. A. GitelsonY. J. Kaufman,
“MODIS NDVI optimization to fit the AVHRR data series—spectral considerations,”
Remote Sens. Environ., 66
(3), 343
–350
(1998). http://dx.doi.org/10.1016/S0034-4257(98)00065-0 RSEEA7 0034-4257 Google Scholar
B.-C. Gao,
“A practical method for simulating AVHRR-consistent NDVI data series using narrow MODIS channels in the 0.5–1.0 μm spectral range,”
IEEE Trans. Geosci. Remote Sens., 38
(4), 1969
–1975
(2000). http://dx.doi.org/10.1109/36.851778 IGRSD2 0196-2892 Google Scholar
K. P. GuntherS. W. Maier,
“AVHRR compatible vegetation index derived from MERIS data,”
Int. J. Remote Sens., 28
(3–4), 693
–708
(2007). http://dx.doi.org/10.1080/01431160600815541 IJSEDK 0143-1161 Google Scholar
H. YoshiokaT. MiuraA. R. Huete,
“An isoline-based translation technique of spectral vegetation index using EO-1 hyperion data,”
IEEE Trans. Geosci. Remote Sens., 41
(6), 1363
–1372
(2003). http://dx.doi.org/10.1109/TGRS.2003.813212 IGRSD2 0196-2892 Google Scholar
H. YoshiokaT. MiuraK. Obata,
“Derivation of relationships between spectral vegetation indices from multiple sensors based on vegetation isolines,”
Remote Sens., 4
(3), 583
–597
(2012). http://dx.doi.org/10.3390/rs4030583 17LUAF 2072-4292 Google Scholar
H. Yoshioka,
“Vegetation isoline equations for an atmosphere-canopy-soil system,”
IEEE Trans. Geosci. Remote Sens., 42
(1), 166
–175
(2004). http://dx.doi.org/10.1109/TGRS.2003.817793 IGRSD2 0196-2892 Google Scholar
A. R. Huete,
“A soil-adjusted vegetation index (SAVI),”
Remote Sens. Environ., 25
(3), 295
–309
(1988). http://dx.doi.org/10.1016/0034-4257(88)90106-X RSEEA7 0034-4257 Google Scholar
Z. Jianget al.,
“Development of a two-band enhanced vegetation index without a blue band,”
Remote Sens. Environ., 112
(10), 3833
–3845
(2008). http://dx.doi.org/10.1016/j.rse.2008.06.006 RSEEA7 0034-4257 Google Scholar
F. BaretG. Guyot,
“Potentials and limits of vegetation indices for LAI and APAR assessment,”
Remote Sens. Environ., 35
(2–3), 161
–173
(1991). http://dx.doi.org/10.1016/0034-4257(91)90009-U RSEEA7 0034-4257 Google Scholar
H. YoshiokaA. R. HueteT. Miura,
“Derivation of vegetation isoline equations in red-NIR reflectance space,”
IEEE Trans. Geosci. Remote Sens., 38
(2), 838
–848
(2000). http://dx.doi.org/10.1109/36.842012 IGRSD2 0196-2892 Google Scholar
H. Yoshiokaet al.,
“Analysis of vegetation isolines in red-NIR reflectance space,”
Remote Sens. Environ., 74
(2), 313
–326
(2000). http://dx.doi.org/10.1016/S0034-4257(00)00130-9 RSEEA7 0034-4257 Google Scholar
F. BaretS. JacquemoudJ. F. Hanocq,
“The soil line concept in remote sensing,”
Remote Sens. Rev., 7
(1), 65
–82
(1993). http://dx.doi.org/10.1080/02757259309532166 RSRVEP 0275-7257 Google Scholar
S. Jacquemoudet al.,
“PROSPECT + SAIL models: a review of use for vegetation characterization,”
Remote Sens. Environ., 113
(Suppl. 1), S56
–S66
(2009). http://dx.doi.org/10.1016/j.rse.2008.01.026 RSEEA7 0034-4257 Google Scholar
J.-B. Feretet al.,
“PROSPECT-4 and 5: advances in the leaf optical properties model separating photosynthetic pigments,”
Remote Sens. Environ., 112
(6), 3030
–3043
(2008). http://dx.doi.org/10.1016/j.rse.2008.02.012 RSEEA7 0034-4257 Google Scholar
W. Verhoefet al.,
“Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies,”
IEEE Trans. Geosci. Remote Sens., 45
(6), 1808
–1822
(2007). http://dx.doi.org/10.1109/TGRS.2007.895844 IGRSD2 0196-2892 Google Scholar
E. F. Vermoteet al.,
“Second simulation of the satellite signal in the solar spectrum, 6S: an overview,”
IEEE Trans. Geosci. Remote Sens., 35
(3), 675
–686
(1997). http://dx.doi.org/10.1109/36.581987 IGRSD2 0196-2892 Google Scholar
A. R. HueteL. FerreiraT. Miura,
“LBA-ECO LC-19 Field Measurements 2002: Biophysical & Soil Parameters,”
in National Institute for Space Research (INPE/CPTEC),
(2008). Google Scholar
C. O. Justiceet al.,
“Land and cryosphere products from Suomi NPP VIIRS: overview and status,”
J. Geophys. Res. Atmos., 118
(17), 9753
–9765
(2013). http://dx.doi.org/10.1002/jgrd.v118.17 JGRDE3 0148-0227 Google Scholar
BiographyKenta Obata is a postdoctoral fellow in the Department of Natural Resources and Environmental Management at the University of Hawaii at Manoa. He received his MS and PhD degrees in information science and technology from Aichi Prefectural University, Aichi, Japan, in 2008 and 2010, respectively. His research interests include intersensor calibration of biophysical retrievals and spectral mixture analysis. Tomoaki Miura is an associate professor in the Department of Natural Resources and Environmental Management at the University of Hawaii at Manoa. He received his MS degree in resource management from the University of Nevada, Reno, in 1996 and his PhD degree in soil, water, and environmental science from the University of Arizona in 2000. His current research interests include satellite vegetation index data product continuity, vegetation index science algorithm development, tropical phenology, and societal impacts on land use changes in the Pacific region. Hiroki Yoshioka is a professor in the Department of Information Science and Technology at Aichi Prefectural University, Aichi, Japan. He received his MS and PhD degrees in nuclear engineering from the University of Arizona, Tucson, in 1993 and 1999, respectively. His research interests include cross-calibrations of satellite data products for continuity and compatibility of similar data sets, development of canopy radiative transfer models and their inversion techniques. Alfredo R. Huete is currently a professor with the Plant Functional Biology and Climate Change Cluster, University of Technology, Sydney, Australia. He received his MSc degree from the University of California, Berkeley, and his PhD degree from the University of Arizona, Tucson. His research interests include understanding ecosystem functioning and vegetation-climate interactions with satellite remotely sensed measurements, with particular emphases in relating biome seasonal shifts in response to climate forcings, land use activities, and their coupling to carbon and water models. He is a member of the Moderate Resolution Imaging Spectroradiometer Science Team and other satellite programs, in which he is involved in the development and validation of the global vegetation index products for land monitoring and climate studies. He has over 100 research publications, a book, and over 20 chapter contributions on remote sensing advancements in characterizing vegetation systems. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

