|
|
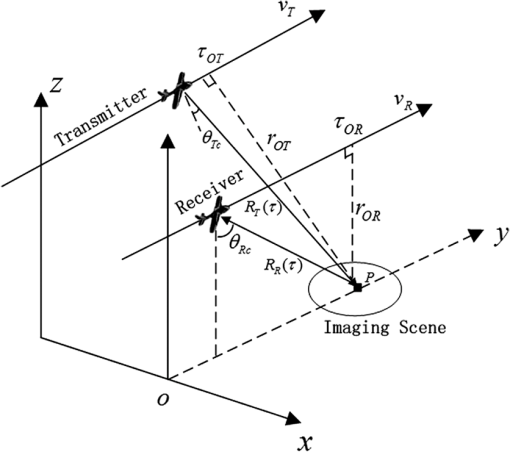
1.IntroductionBistatic forward-looking synthetic aperture radar (BFSAR) has two platforms installed with a transmitter and receiver, respectively. Despite the separation of the two platforms, the BFSAR can still achieve a high azimuth resolution if a forward-looking geometry is used. Forward-looking imaging is highly desirable in some applications, but it has been a blind sector for monostatic synthetic aperture radar (SAR)1–3 for a long time. Therefore, BFSAR has recently received considerable attention. The peculiarity and feasibility of BFSAR was studied in detail.4–6 Through the exploration of the limitation and potential of BFSAR, the best forward-looking geometry was proposed for achieving a high-resolution image. Moreover, some BFSAR experiments were carried out and the exciting imaging results were obtained.7–10 However, we can find that the imaging algorithms used in these experiments are mostly backprojection algorithms (time-domain algorithms). The time-domain algorithm can work well in arbitrary flight trajectories and no approximation is taken. However, it has a high computational cost and is not available for real-time imaging applications. Therefore, it is urgent to develop new frequency-domain imaging algorithms. Some theories of imaging algorithms for BFSAR have been reported. Based on the extended Loffeld’s bistatic formula (ELBF) method,11 a range-Doppler algorithm is developed.12 But the ELBF method has its limitations in representing the bistatic point target reference spectrum (BPTRS). A chirp scaling algorithm (CSA) based on the method of Legendre polynomial extension was also proposed.13 The accuracy of this imaging solution is decided by the reserved order of an expending Taylor series. With the keystone transform method, a nonlinear chirp scaling algorithm for one-stationary BFSAR was derived.14 In addition, a modified Omega-k algorithm was also reported.15 To develop new frequency-domain imaging algorithms, we have to obtain the BPTRS of BFSAR first. The BPTRS derived by the method of series reversion (MSR)16 has a good focusing performance for the general bistatic configuration, even for extreme squint cases. Due to the series form, it is not easy for MSR to be used for imaging algorithm deduction, especially for chirp scaling and Omega-k algorithms.17 The Loffeld’s bistatic formula (LBF) was first introduced in Ref. 18. In LBF, the contributions of the transmitter and receiver to the total Doppler frequency are assumed to be the same. This assumption results in the failure of LBF in the extreme configuration (i.e., spaceborne/airborne configuration). The ELBF11 was proposed, but it cannot handle the large squint cases of bistatic SAR. The zeroth-order ELBF19 obtained two gradient equations to solve the Doppler contributions. However, the method would lead to some degradation when it is used in cases with extreme squint or with forward-looking cases to some extent.17 In this paper, a modified Loffeld’s bistatic formula (MLBF) has been proposed. Compared to LBF18 and ELBF,11 it can precisely represent the bistatic point target reference spectrum of bistatic forward-looking SAR. Then, a CSA based on BPTRS was derived. Because CSA is free of interpolation, this algorithm has an obvious superiority in efficiency. Finally, numerical simulations were carried out to validate the focusing solution for BFSAR. 2.Modified Loffeld’s Bistatic FormulaThe geometry configuration of BFSAR is shown in Fig. 1. The transmitter works in the side-looking mode and the receiver works in the forward-looking mode, respectively. The two platforms move along the axis. The mathematical symbols and their definitions used in Fig. 1 are given as follows:
The instantaneous slant ranges from the transmitter and receiver to the point target P at time are defined as Hence, the echo data from target P after demodulation are where and are window functions for range and azimuth, respectively; is the backscattering coefficient of the point target P; is the central azimuth time of the composite azimuth antenna pattern; is the velocity of light; and are the carrier frequency and wavelength; and is the frequency modulated rate of linear frequency modulation signal.Taking a two-dimensional FFT for Eq. (3), we get where and represent the range and azimuth frequency variables; the bistatic phase is given as follows:From Eqs. (4) and (5), we can see that the bistatic phase term contains a double square root and is included in the integral. It is difficult to obtain the BPTRS from Eq. (4) by directly applying the stationary phase.20,21 Thus, we split the bistatic phase term, Eq. (5), into two components as follows: where and are the phase terms contributed by the transmitter and receiver, respectively. and represent the instantaneous azimuth frequencies for the transmitter and receiver, respectively. In the LBF method,18 it is assumed that the contributions of the transmitter and receiver to the azimuth modulation are the same. The assumptions are shown as follows:However, the real azimuth modulations of the transmitter and receiver are not equal at all when the LBF is used in the extreme configuration (i.e., spaceborne/airborne configuration). Then, ELBF11 formulates and as follows: where and are the weighting factors, which are defined as the ratio of the time-bandwidth product (TBP) of transmitter and receiver to the total TBP. However, the ELBF shows a limitation in the high squint cases of bistatic SAR since the effect of squint angles on the instantaneous Doppler frequency is neglected.The zeroth-order ELBF method19 makes the result of Eq. (12) as small as possible. where and are the transmitting and receiving points of stationary phases (PSPs). The variables and are included in and , respectively. This equation does not have an analytical solution, and an approximate solution can be found by using the least square method. The main idea of zeroth-order ELBF is to approximate the difference between the transmitting and receiving PSPs to zero. However, in this method, only the contributions of zeroth-order Doppler frequencies are considered. This would lead to some degradation when the method is used in forward-looking cases with large forward-looking angles.In this paper, we try to solve the instantaneous azimuth frequencies and directly. Here, we redraw the geometries of the flight tracks of the transmitter and receiver, as shown in Fig. 2. Fig. 2The flight geometry of transmitter and receiver. (a) The geometry of transmitter’s track. (b) The geometry of receiver’s track. 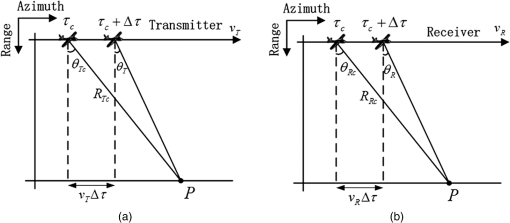 In Fig. 2, and are the instantaneous squint and forward-looking angles at time ; and are the slant ranges of the transmitter and receiver at the composite beam center crossing time . Suppose the transmitter and receiver both start flying at time ; after time we can get the following relationship: Meanwhile, the two instantaneous Doppler frequencies satisfy the following relationship: Solving the equations composed by Eqs. (13) and (14), we can get the analytic expression of the frequencies and . We expand and in their Taylor series as follows: whereCombined with Eqs. (13) and (14), coefficients , can be obtained, then we get the analytic expressions of the frequencies and . Although the results in Eq. (15) are more precise than those in Ref. 19 due to the high-order term in Eq. (15), the complexity of the method is greatly increased. It would make present difficulties when we derive the chirp scaling algorithm later. Therefore, some linear approximations are used here to solve Eqs. (13) and (14). We expand and in their Taylor series at and , respectively, and only reserve the first-order term. Substituting Eq. (17) into Eq. (13) and combining Eq. (14), the equations are solved as follows: Although linear approximation is used, the max error made by this approximation (with Table 1 simulation parameters, which is discussed later in this paper, the forward-looking angle of the receiver is 45 deg) is . Therefore, the error can be ignored and Eq. (18) can precisely present the contributions of the transmitter and receiver to the total azimuth modulation. After obtaining the instantaneous azimuth frequency of the transmitter and receiver, we expand Eqs. (7) and (8) at their points of the stationary phase and . The expanded series are truncated at the second-order term, given as whereTable 1System parameters in parallel tracks.
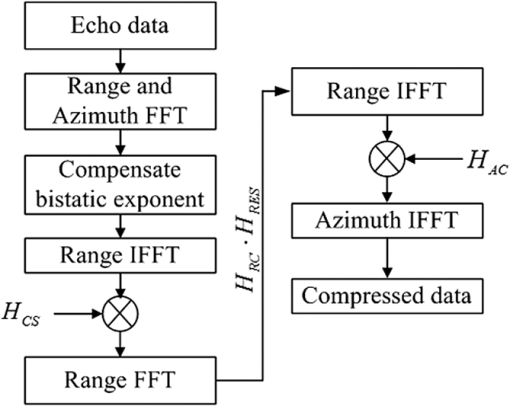
Substituting Eqs. (6), (19), and (20) into Eq. (4), we get Applying stationary phase techniques to the last exponent in Eq. (24), we get the bistatic stationary phase . Finally, we get the BPTRS of the BFSAR. wherecan be considered as the quasi-monostatic phase term, and is defined as the bistatic deformation phase term. Before implementing an imaging algorithm, the bistatic deformation phase term should be compensated. The method proposed above can be considered as an MLBF. 3.CSA for the Bistatic Forward-Looking SAR ProcessingInstead of interpolation, chirp phase multiplication is used in CSA to correct the range cell migration (RCM). It is an efficient algorithm. However, due to the unknown scaling factor, it is complex to derive CSA based on the BPTRS obtained by the MLBF. After compensating the bistatic deformation phase term, we transform Eq. (26) into a range-Doppler domain and obtain the expression as whereIn Eq. (29), the frequency-modulated rate in range is changed by the coupling of the range and azimuth, and the new chirp rate in range-Doppler domain is given as In Eq. (29), is the range migration of a target and is defined as We assume the range chirp scaling function for the BFSAR as follows: where is the unknown scaling factor. is the range migration of the reference target, given asIn Ref (41), and are the closest ranges from the transmitter and receiver to the reference target. (The target located at the middle of the imaging scene is usually chosen as the reference target.) We multiply Eq. (29) by Eq. (39) and implement FFT in the range direction, and then get In Eq. (41), we can clearly see that the total RCM is Because the translational invariant case is used in this paper, we make some linear approximations.12 The approximations are given as where , , and are all coefficient factors. Therefore, we can transform the total RCM as follows: where the last term of the RCM is a range variant term. In order to remove the range variant of the total RCM on the Doppler frequency, we let Then, the analytic formula of the scaling factor is obtained asTherefore, after substituting Eq. (47) into Eq. (41), we can rewrite Eq. (41) without unknown variables. Then, we use the following matching filters to complete the image focusing: where is used for range compression (RC), the second range compression, and the bulk range cell migration correction; is used for azimuth compression; and is used to remove the residual phase term introduced by the chirp scaling multiplication. The corresponding block diagram of the CSA for the BFSAR is shown in Fig. 3.4.Simulation ResultsIn order to verify the focusing solution for the BFSAR, two simulation experiments are carried out in this section. The first experiment is to determine whether the BPTRS obtained by the MLBF is appropriate for the BFSAR case and to simultaneously compare the performance of the MLBF with those of other proposed methods. The second experiment is to validate the effectiveness of the proposed CSA. The simulation parameters are listed in Table 1. We use the analytical BPTRS to focus the BPTRS obtained by LBF,18 ELBF,11 MLBF, and the spectra derived from the MSR using the fourth-order expansion.16 The focusing results are shown in Fig. 4. Fig. 4Focusing results. (a) Processing result using Loffeld’s bistatic formula (LBF). (b) Processing result using extended LBF. (c) Processing result using modified LBF (MLBF). (d) Processing result using method of series reversion. (e) Comparison results of the azimuth profiles obtained from Figs. 4(c) and 4(d). 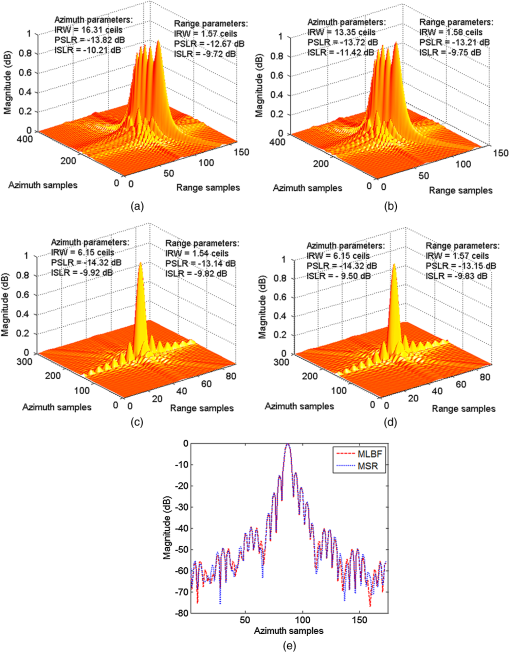 From Figs. 4(a) and 4(b), we can see that the LBF and ELBF have severe degradation in the azimuth direction. They are not appropriate for bistatic forward-looking SAR cases. In general, the LBF method and ELBF method reach their limit when the forward-looking angle is 30 and 40 deg, respectively. Figures 4(c) and 4(d) reveal that MLBF and MSR are all focused on the point target. Furthermore, Fig. 4(e) shows the azimuth profiles of the MLBF and MSR. It is clear that the method proposed in this paper agrees with the MSR. However, the resulting accuracy of the spectrum from the MSR is dependent on the number of terms in the expansion. Here, we use the fourth-order expansion of the MSR. However, the spectrum of the MLBF is a closed form with a second term and still has a good performance. In addition, it is not easy for the MSR to be used for imaging algorithm deduction. The CSA imaging results are shown in Fig. 5. Fig. 5CSA imaging results based on the bistatic point target reference spectrum obtained by MLBF. (a) The locations of simulated targets. (b) The contours of final imaging result with 30 dB dynamic range. (c) The azimuth profile of the target P9. (d) The range profile of the target P9. 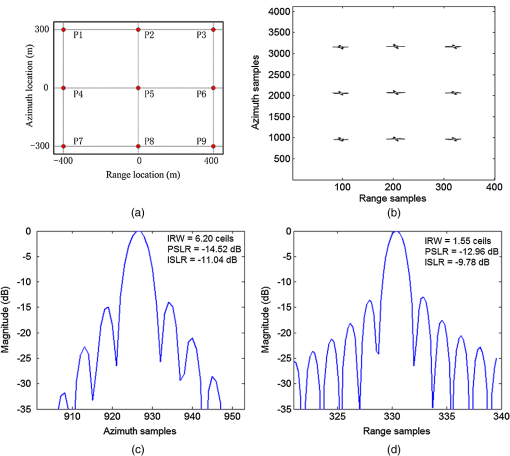 Figure 5(a) shows the locations of the simulated targets, where the distances between two adjacent targets along the range and azimuth directions are, respectively, 400 and 300 m. Figure 5(b) represents the contours of the final imaging result. The dynamic range shown in this picture is 30 dB. In order to further evaluate the imaging quality, Figs. 5(c) and 5(d) present the impulse profiles of the target P9 in the azimuth and range directions, respectively. The peak sidelobe ratio (PSLR) of the azimuth profile is , and the integrated sidelobe ratio (ISLR) is . The PSLR of the range profile is , and the ISLR is . More image quality parameters are listed in Table 2. The ideal impulse response width (IRWs) of the azimuth and range are 6.04 and 1.52 ceils (or samples), respectively. We can find that all the targets are well focused. Table 2Image quality parameters.
PSLR, peak sidelobe ratio; ISLR, integrated sidelobe ratio. 5.ConclusionsA focusing solution for bistatic forward-looking SAR was presented in this paper. First, an MLBF was proposed to obtain the BPTRS. Then, a chirp scaling algorithm based on the BPTRS was derived. Compared to other imaging algorithms, CSA is free of interpolation. Finally, two simulation experiments were carried out to validate the focusing solution. The simulation results showed that the BPTRS obtained by the MLBF was more precise than the LBF and ELBF, and that the focusing capability of the derived CSA is high. AcknowledgmentsThis paper is supported by the PhD programs foundation of Ministry of China (Grant No. 20113219110018), the Ministry Pre-research Foundation (Grant No. 9140A07010713BQ02025), National Natural Science Foundation of China (Grant No. 61302188), and Natural Science Foundation of Jiangsu Province (Grant No. BK20131005). ReferencesO. DoganM. Kartal,
“Efficient stripmap-mode SAR raw data simulation including platform angular deviations,”
IEEE Geosci. Remote Sens. Lett., 8
(4), 784
–788
(2011). http://dx.doi.org/10.1109/LGRS.2011.2112633 IGRSBY 1545-598X Google Scholar
S. H. ShimY. M. Ro,
“Practical synthetic aperture radar image formation based on realistic spaceborne synthetic aperture radar modeling and simulation,”
J. Appl. Remote Sens., 7
(1), 073494
(2013). http://dx.doi.org/10.1117/1.JRS.7.073494 1931-3195 Google Scholar
Q. Q. PengL. Zhao,
“Novel mixture model for synthetic aperture radar imagery,”
J. Appl. Remote Sens., 6
(1), 063616
(2012). http://dx.doi.org/10.1117/1.JRS.6.063616 1931-3195 Google Scholar
J. BalkeD. MatthesT. Mathy,
“Illumination constraints for forward-looking radar receivers in bistatic SAR geometries,”
in European Radar Conf.,
25
–28
(2008). Google Scholar
J. Wuet al.,
“Bistatic forward-looking SAR: theory and challenges,”
in IEEE Radar Conf.,
1
–4
(2009). Google Scholar
I. Walterscheidet al.,
“Potential and limitations of forward-looking bistatic SAR,”
in IEEE Int. Geoscience and Remote Sensing Symp.,
216
–219
(2010). Google Scholar
J. Wuet al.,
“First result of bistatic forward-looking SAR with stationary transmitter,”
in IEEE Int. Geoscience and Remote Sensing Symp.,
1223
–1226
(2011). Google Scholar
T. Espeteret al.,
“Bistatic forward-looking SAR experiments using an airborne receiver,”
in Proc. Int. Radar Symp.,
41
–46
(2011). Google Scholar
J. Balke,
“SAR image formation for forward-looking radar receivers in bistatic geometry by airborne illumination,”
in IEEE Radar Conf.,
1
–5
(2008). Google Scholar
I. Walterscheidet al.,
“Bistatic spaceborne-airborne forward-looking SAR,”
in 8th European Conf. on Synthetic Aperture Radar,
1
–4
(2010). Google Scholar
R. Wanget al.,
“A bistatic point target reference spectrum for general bistatic SAR processing,”
IEEE Geosci. Remote Sens. Lett., 5
(3), 517
–521
(2008). http://dx.doi.org/10.1109/LGRS.2008.923542 IGRSBY 1545-598X Google Scholar
R. Wanget al.,
“Image formation algorithm for bistatic forward-looking SAR,”
in IEEE Int. Geoscience and Remote Sensing Symp.,
4091
–4094
(2010). Google Scholar
J. Wuet al.,
“Focusing bistatic forward-looking SAR using chirp scaling algorithm,”
in IEEE Radar Conf.,
1036
–1039
(2011). Google Scholar
J. Wuet al.,
“Focusing bistatic forward-looking SAR with stationary transmitter based on keystone transform and nonlinear chirp scaling,”
IEEE Geosci. Remote Sens. Lett., 11
(1), 148
–152
(2014). http://dx.doi.org/10.1109/LGRS.2013.2250904 IGRSBY 1545-598X Google Scholar
H. S. ShinJ. T. Lim,
“Omega-k algorithm for airborne forward-looking bistatic spotlight SAR imaging,”
IEEE Geosci. Remote Sens. Lett., 6
(2), 312
–316
(2009). http://dx.doi.org/10.1109/LGRS.2008.2011924 IGRSBY 1545-598X Google Scholar
Y. L. NeoF. WongI. G. Cumming,
“A two-dimensional spectrum for bistatic SAR processing using series reversion,”
IEEE Geosci. Remote Sens. Lett., 4
(1), 93
–96
(2007). http://dx.doi.org/10.1109/LGRS.2006.885862 IGRSBY 1545-598X Google Scholar
J. Wuet al.,
“A new look at the point target reference spectrum for bistatic SAR,”
Progr. Electromagn. Res., 119 363
–379
(2011). http://dx.doi.org/10.2528/PIER11050704 PELREX 1043-626X Google Scholar
O. Loffeldet al.,
“Models and useful relations for bistatic SAR processing,”
IEEE Trans. Geosci. Remote Sens., 42
(10), 2031
–2038
(2004). http://dx.doi.org/10.1109/TGRS.2004.835295 IGRSD2 0196-2892 Google Scholar
R. Wanget al.,
“Extending Loffeld’s bistatic formula for general bistatic SAR configuration,”
IET Radar Sonar Navig., 4
(1), 74
–84
(2010). http://dx.doi.org/10.1049/iet-rsn.2009.0099 1751-8784 Google Scholar
C. Maet al.,
“Focusing bistatic forward-looking synthetic aperture radar based on modified hyperbolic approximating,”
Acta Physica Sinica, 63
(2), 028403
(2014). http://dx.doi.org/10.7498/aps.63.028403 WLHPAR 1000-3290 Google Scholar
R. Wanget al.,
“Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase,”
IEEE Trans. Geosci. Remote Sens., 49
(10), 3504
–3520
(2011). http://dx.doi.org/10.1109/TGRS.2011.2129573 IGRSD2 0196-2892 Google Scholar
BiographyChao Ma received his BS degree from Hubei Engineering University, Hubei, China, in 2010. He is currently working toward his PhD degree in information and communication engineering at the Nanjing University of Science and Technology, Jiangsu, China, and is trained in the Institute of Electronic Engineering and Optoelectronic Technology. His research interests include synthetic aperture radar (SAR) signal processing and short-range imaging. Hong Gu received his MS degree from Nanjing University of Science and Technology, Jiangsu, China, in 1991 and his PhD degree from Xidian University, Shanxi, China, in 1995. He is currently a professor, a Chinese Institute of Electronics senior member, and a member of the radar branch of the Jiangsu Electronic Society. His research interests include noise SAR, radar signal processing and information systems. Weimin Su received his PhD degree from Nanjing University of Science and Technology, Jiangsu, China, in 1998. He is currently a professor, a senior member of the Chinese Institute of Electronics, a member of the Signal Processing Society of China, and a liaison of Nanjing University of Science and Technology, Jiangsu, China. His research interests include advanced SAR systems and signal processing technology. Chuanzhong Li received his BS degree from Nanjing University of Science and Technologu, Jiangsu, China, in 2010. He is currently working toward his PhD degree in information and communication engineering at Nanjing University of Science and Technology, Jiangsu, China. His research interests include radar signal processing and noise SAR imaging. Jinli Chen received his PhD degree from Nanjing University of Science and Technology, Jiangsu, China, in 2010. He is currently working in the Nanjing University of Information Science and Technology as a lecturer. His research interests include multiple input multiple output (MIMO) radar signal processing and high-speed moving target detecting. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||