|
|
1.IntroductionThe primary focus of several aircraft and space-based instruments is to assess the global distribution of greenhouse gases including carbon dioxide () and, more importantly, the associated time varying fluxes. Among these are the current “Greenhouse gases Observing SATellite,”1–3 that hosts a passive multiband Fourier transform spectrometer designed to measure atmospheric column abundances of and , and the recently launched orbiting carbon observatory mission,4 whose multiband grating spectrometers will provide data to characterize sources and sinks on regional scales. In addition, a number of potential missions are in the planning phase, such as the NASA Decadal Survey Active Sensing of Emissions over Nights, Days, and Seasons (ASCENDS) mission, which will employ active technologies, such as laser differential absorption spectroscopy (LAS), to quantify global mixing ratio () column amounts. The preformulation phase of this effort is currently being supported by a number of aircraft-based instruments and technology demonstrations.5–7 Although the active sensing approaches have some significant benefits in that they enable the measurements under nonsunlit conditions and are potentially less susceptible to interference due to clouds and aerosols, they and their passive counterparts face similar technological challenges which must be addressed in order to meet their stringent measurement goals and objectives. Not only there are a number of technological issues, e.g., hardware qualification, mass, and power constraints that must be considered in any successful design, but also there are a number of atmospheric state and spectroscopy issues that impact end-to-end performance and overall measurement accuracy. Among the latter are the interplay between uncertainties in the observed atmospheric state and its impact on the spectroscopic variability due to pressure, temperature, interference from other gaseous species, and the associated altitude-dependent measurement weighting functions. Desired product accuracies of to 2 ppm for (Refs. 8 and 9) result in derived requirements for both the sensor (i.e., instrument noise) and the data processing (overall processing algorithm accuracy). One such challenge that faces both the passive and the active approaches is to understand the impact of required ancillary information on the accuracy and precision of the retrieved column values. In particular, uncertainties in global surface pressure drive estimates of dry air column density. The vertical distribution of temperature and moisture also impacts estimates of dry air column density as well as the associated spectroscopy and radiative transfer. Because of the stringent measurement requirements, this overall “atmospheric uncertainty” usually represents a large fraction of the overall sensor/system error budget. Line selection is a critical part of any such instrument design that must meet or exceed the stringent measurement requirements. This work outlines a simulation-based method for assessing the impact of “atmospheric uncertainty,” hereafter referred to as “noise,” due to uncertainties in temperature and moisture profiles and surface pressure on LAS-based measurements of columns using the integrated path differential absorption (IPDA) technique (The term “atmospheric noise” is often used to refer to the radio waves generated by lightning during thunderstorms. However, in the context of a sensor system error budget, the error due to uncertainty in the assumed atmospheric state can also be considered as a “noise” term. In this paper, we refer to the “atmospheric uncertainty” as “noise.”).6 To illustrate this methodology we provide results from this analysis method for multiple absorption features in the region described in prior works5,6 as suitable absorption lines for estimating column amounts, and a single feature in the region proposed for estimating surface pressure via differential absorption due to oxygen (). We have limited the analyses to clear-sky conditions because the goal of this work is to design and demonstrate a consistent mechanism for parameterizing the and the column measurement uncertainties due to atmospheric state uncertainty and to allow for an objective means of selecting spectral lines/regions as part of a mission design. Although this work was conducted with LAS systems that utilize single on-line/off-line wavelength pairs, our analysis could be applied to systems that utilize multiple on/off-line wavelength pairs. With only slight modifications, this technique would also be applicable to understanding uncertainties in clouds, aerosols, and surface topography. Such analyses are the focus of on-going/future development efforts. The goal of this work is to assess the impact of uncertainties in atmospheric temperature, moisture, and surface pressure knowledge on the two observed quantities ( differential absorption cross section and differential optical depth) that provide an estimate of . Like their passive counter parts, these measurements will also be impacted by a number of other atmospheric parameters such as aerosols and clouds. However, the impacts of these quantities on the measured values are highly dependent on instrument implementation and are beyond the scope of this work. It is most likely that any final implementation would include extensive cloud screening to mitigate the impact of clouds on the desired clear-sky retrievals. Second partial paths contamination due to partial column information introduced by reflections off of cloud decks or aerosols may be mitigated in a pulsed implementation using range gating to distinguish returns from clouds versus surface terms.5 Range information to cloud decks or aerosol layers can also be obtained with a continuous wave system that uses swept-frequency modulation techniques.6 The meteorological uncertainties characterized in this work would factor into a comprehensive error budget for any IPDA instrument measurements. 2.Differential Absorption Measurement TechniqueThis work outlines a method for assessing the impact of atmospheric state uncertainty for a laser-based differential absorption measurement system. These measurements of column and amounts are derived from ratios of transmittance values or differences in optical depths obtained by measuring the absorption for a set of independent laser lines. The quantities represent the observed laser energy that is transmitted from the observer to the surface of the earth and reflected back to collocated receivers. In the simplest case, these ratios/differences are computed for two independent wavelengths, one traditionally located somewhere “on” the spectral absorption feature of interest, and the other located “off” the spectral absorption line of interest. The on-line values provide a measure of relative absorption/transmission due the average gas column density, and the off-line values are a relative measure of any background absorption. The ratio of these two values provides a measure of absolute column density. For example, the observed differential optical depth, , associated with a given spectral feature as illustrated in Fig. 1, is also given by where is the differential absorption cross section, is the number density, is the local acceleration due to gravity, is the molecular mass of dry air (, where is Avogadro’s number), is the local specific humidity, is the surface pressure, and represent the on/off-line wavelengths. is given by where represents the residual observed differential optical depth due to other species in the region of interest. Optimally, approaches zero in the case where the region of interest is void of other absorption features, e.g., water vapor and other trace gases. The measurement error terms are not only driven by the instrument design but also the ancillary meteorological data employed in the retrieval process and the interplay between the two. Both and vary as a function of pressure and temperature. As illustrated by these equations, the accuracy of retrieved values depends not only on the error characteristics of the observed but also on the ability to accurately characterize the P, T, and WV concentrations along the observed path. In the case of global space-based monitoring systems, retrievals of typically rely on P/T/WV values derived from meteorological analyses that combine atmospheric general circulation models with assimilation of both ground-based measurements, e.g., rawinsonde observation (RAOB) and hourly surface weather observations, and satellite observations to globally estimate the atmospheric state. This work addresses the impact of uncertainties in atmospheric temperature, moisture, and surface pressure knowledge on the two observed quantities that provide an estimate of as given in Eq. (2). These parameters are the column mixing ratio and the dry air surface pressure, which can be derived from the observed surface pressure and the water vapor mixing ratio profile. Similar to their passive counterparts, these measurements are also impacted by a number of other atmospheric parameters such as aerosols and clouds. However, the impact of these parameters on the measured quantities is highly dependent on instrument implementation and is beyond the scope of this work.Fig. 1Ensemble RMS differences between rawinsonde observation measurements and corresponding numerical weather prediction (NWP) analysis temperature (a) and water vapor mixing ratio (b) profiles. Each panel illustrates the errors for 0Z and 12Z NWP analysis fields respectively. The black lines represent the respective RMS differences as a function of pressure and the blue lines denote the RMS as a function of vertical height from the surface. 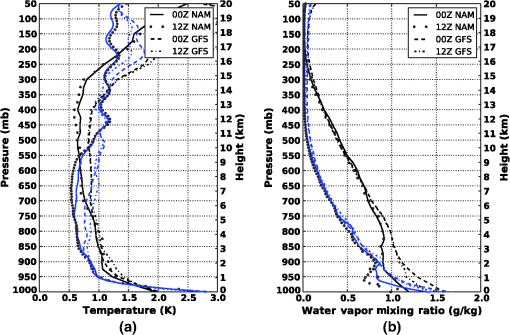 The dependency on surface pressure in Eq. (2) assumes the use of a model meteorological value that includes influences due to water vapor. Errors in meteorological data (T/WV/P) may be reduced by using an estimation of surface pressure derived from a second measurement of the differential optical depth due to . For this reason, an analysis of the column amount and derived surface pressure is included in this study. In the case of surface pressure derived from measurements, Eq. (2) becomes 3.MethodThe analyses implemented in this work utilized the ratio of the measurement signal to the signal uncertainty due to imperfect knowledge of the atmospheric state (noise). These quantities were developed using the following simulation paradigm:
The details of each of these steps are given in the following sections. This process was initiated by developing a set of matched pairs of observations and model vertical temperature, moisture, and surface parameters derived from RAOB (Ref. 11) and NWP model fields collected both over the continental United States as well as on a global basis for representative periods between July 2011 and July 2012. The representative time periods were chosen to include data from all seasons as well as both daytime and nighttime observations. The RAOBs were obtained from publically available sources and the matching model data were extracted from both the 12-km North American mesoscale model (NAM)12 and ½ deg global forecast system (GFS)13 analysis fields. The NAM was chosen to represent the uncertainty statistics associated with a high spatial resolution model for a well-instrumented area, and the GFS fields were chosen to illustrate the errors associated with a courser global domain. Only 0-h forecasts or model analysis fields were selected in this work to describe the model error characteristics based on the assumption that any operational retrieval system would either acquire data from an external source or employ an -dimensional variational data assimilation system to minimize the impact due to uncertainties in the atmospheric state. Although RAOBs are by no means an absolute representation of the atmospheric state at any point,14 they do provide a consistent measure that can be compared with NWP data for statistical purposes. The matching NWP profiles were selected using a nearest neighbor approach based on the RAOB station location and contained vertical temperature and moisture, relative humidity (RH) profiles on a fixed pressure grid as well as surface parameters (temperature, RH, surface pressure, and station height). A conservative quality control scheme was used to screen out RAOB with missing data and those in cloudy conditions based on the model cloud fraction and RAOB upper-air water vapor. The RMS differences as a function of pressure level for the resulting temperature and RH profiles for the ensemble set are shown in Fig. 1. This figure illustrates the vertical distribution of errors in both temperature and water vapor between the nominal surface (1000 mbar) and (50 mbar) for both the 0Z and 12Z analysis. This figure shows the vertical error distribution as a function of both pressure and height above the surface for the NAM and the GFS profile databases used in this study. The temperature errors range from 1 to 1.2 K in the troposphere to a maximum of 2 to 3 K at the surface. The errors at the surfaces are due to, among other things, the mismatches between observer height and model grid cell height. The water vapor mixing ratios root mean squared error (RMSE) values ranged from near zero in the upper troposphere to 0.5 to in the 2 to 5-km range and 1.5 to at the surface. Although this set of matched observation and model profile pairs do not provide an adequate estimate of the extremes, they do provide a systematic method for quantifying the statistical mean impact of these uncertainty terms on measurement error. A similar approach was taken to assess the global variance in surface pressure. Observed surface pressure values were extracted from airport and/or permanent surface weather observation station reports (METAR) for the same contiguous United States (CONUS) and global regions described above along with their corresponding NWP model values. The NWP model values were corrected to the observed station height using a standard lapse rate relationship. The resulting value for the CONUS region was and the value was 2.1 mbar. The global region exhibited a value of 0.8 mbar and a value of 1.7 mbar, respectively. Globally, these observations showed no significant biases and only slight seasonal variation in standard deviations. The standard deviation varied as expected as a function of hemispheric region. In this study, the uncertainties in surface pressure knowledge were simulated by adding random variables drawn from normal distributions with standard deviations of 1 mbar to represent a nominal case and of 2 mbar to explore a more extreme environment. The atmospheric state vector pairs were combined with a nominal vertical profile with a constant concentration of 385 ppm and input into the LBLRTM (Ref. 10) to construct sets of simulated optical depths (typically referred to as “”) over a predefined range of wavenumbers. LBLRTM optical depths are computed from Voigt line shape functions at atmospheric levels and with a continuum model that includes self- and foreign-broadened water vapor as well as continua for , , , and extinction due to Rayleigh scattering. The version used in the study included 2012 updates to the line parameters and coupling coefficients based on the work of Devi et al.,15,16 the line parameters based on HITRAN (Ref. 17), and additional quadrupole parameters between 7571 and . For each of 2500 profile pairs a set of simulated truth, signal, and model values of optical depth were computed. The RAOB data were used to simulate the “true” optical depths observed by the sensor and the model profiles were used to construct the “model” optical depths that would be used in the retrieval approach given an estimate of the atmospheric state. In addition, a set of “signal” optical depths were constructed based on the “truth” profiles and either an augmented profile or a change in surface pressure. In the case, the nominal profile was augmented by adding a predefined concentration to each layer between the surface and simulated observation height. In the case, the observed surface pressure was adjusted by modifying the surface height to match the desired surface pressure. In this case, the signal pressure values were assumed to be less than the observed or model values to prevent the use of subsurface profile values. In all cases, the observed path length, i.e., the height between the observer and the surface, was held fixed to eliminate changes in optical depths due to path length. These values of were then employed to generate spectrally dependent atmospheric uncertainties (noise) and average signal values given a defined set of differential wavelength pairs. This work assumes that retrieved column or surface pressure values are derived from the difference in optical depths between the absorption at an “off-line” wavelength whose absorption is dominated by the continuum or constituents other than the feature of interest, and a value at an “on-line” wavelength whose absorption is primarily driven by the feature of interest. Although this approach does not address all retrieval methods or observational techniques that employ multiple measurements along a given absorption feature, it does provide metric values that can, in general, be used to constrain the fit between the observed data and RT modeled values. The noise in the measurements of associated with uncertainties in the atmospheric state at each spectral sample in the given simulated waveband was computed as the RMS error defined as the differences between the simulated true values and the NWP model based values of . These differences in optical depths, for a given off-line (), were calculated as and where is the observed or true optical depths derived from the RAOB data. In the noise case, is computed based on derived from the NWP model data, and the estimated noise values as a function of wavelength are given as the RMS error of : where is the number of profiles in the match pair dataset. In the signal case, the values are derived from atmospheric state variables based on the RAOB data plus an augmented column or surface pressure value. The resulting signal term is then given as the absolute average over the ensemble set of :In this study, the differential signal and the noise spectra were computed for three regions near , and a single band of interest near , consistent with the sensor simulations described in Ref. 18. Each band was 300-pm wide and had center wavelengths at , 1.5723, and (6327.06095, 6359.96733, and ) for the bands, and the center of the trough—the mid-point between two closely spaced absorption features—at () for the band. Two observational scenarios were constructed to evaluate observations from an airborne instrument and those for a space-based mission, with both scenarios developed based on a nadir viewing geometry. The airborne configuration assumed a 5-km observation altitude, whereas the space-based scenario was based on a 20-km observation altitude. Although it is well understood that the space-based scenario covers only a fraction of the path associated with any proposed satellite viewing geometry, the length selected bounds the limits of the observed and NWP data, and represents the fraction of the atmosphere that has the most severe impact on these measurement techniques. Figure 2 shows representative optical depth values, and an example set of computed signal and noise values is shown in Fig. 3. These figures illustrate how changes in the column and atmospheric pressure () impact the measurement and provide a reference for how large of an atmospheric uncertainty is acceptable. That is, the atmospheric uncertainty must be much less than these changes in and in order to retrieve the desired quantities with the required accuracy. Fig. 2Representative optical depth values for nadir space sensor with 20-km vertical atmospheric path length. values are shown for the absorption feature centered at (a), and the line at (b). The lines represent the optical depth values as a function of wavelength derived from the CONUS North American Mesoscale Model (NAM) data. The notional on- and selected off-line ( offset from line center) positions are illustrated in the graphs as solid vertical lines. 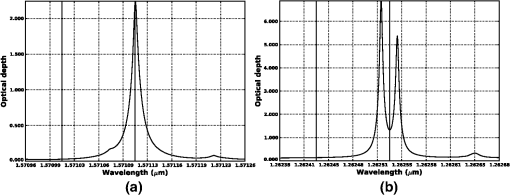 Fig. 3Representative optical depth-derived signal and noise values for nadir space sensor with 20-km vertical atmospheric path length. Signal and noise values for line for absorption feature centered at (a), and the line at (b). The solid lines represent the simulated noise values as a function of wavelength derived from both the CONUS NAM data (red) and the global forecast system (GFS) data (blue). In the case, an additional 1-mbar uncertainty was also introduced. The dashed and dotted lines in the left hand plot represent the average signal given by a 1 and 2 ppm change in column amount, and a 1 and 2 mbar change in surface pressure in the right hand plot. The on- and selected off-line ( offset from line center) positions are illustrated in the graphs as solid vertical lines. 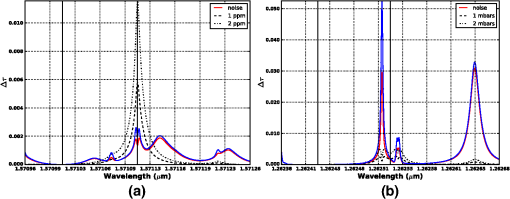 These simulated differential optical depth signal and noise values were then used to compute first-order estimates of expected signal uncertainties (equivalent noise signals) due to uncertainties in temperature, water vapor, and surface pressure. Equivalent noise signal is the relative change in parts per million (or surface pressure in mbar for the case) that is equivalent to the error in retrieved concentration (or surface pressure) due to uncertainties in the knowledge of the atmospheric state variables. The resulting values, in parts per million for the lines and millibar for the case, were computed by first constructing a set of simulated values for signal steps that span the expected noise range. In the case, these signal values ranged from 0 to 10 ppm, and 0 to 5 mbar in the case. Finally, these three-dimensional volumes of optical depths as a function of wavelength and differential-integrated column signal strength were used to derive the equivalent noise signals by interpolating the noise values for a specific on/off-line pair under predescribed noise conditions to the equivalent signal value with the same value. A two-dimensional representation of these results is shown in Fig. 4. This figure illustrates the resulting estimates for noise equivalent signal for both the line at , and the line at given a 20-km nadir viewing geometry. Both figures show the noise equivalent signal for all on/off line combinations for a range at line center for the case and the trough minimum in the case. The uncertainties in these examples were solely derived from uncertainties in temperature and moisture described by the CONUS-based observation and model profile pairs. As expected, both images in this figure are symmetric around the diagonal where the signal is identical for on- and off-line combinations with identical wavelengths. In the case, the noise equivalent signal is at a minimum when the on-line resides at or near the line center and the off-line is placed well within the continuum region. These results are expected since there is no appreciable contamination due to water vapor, and the weighting functions near line center peak higher in the atmosphere and have reduced contributions at the surface. These signal and noise terms formed the basis for a number of analyses designed to assess and quantify the impact of uncertainties in atmospheric state knowledge on estimating or column amounts. Fig. 4Two-dimensional representation of noise equivalent signal for 20-km nadir viewing geometry. Panel (a) illustrates noise equivalent signals for line at , and panel (b) shows those for the line at . Noise equivalent signals were constructed by 4 interpolating noise to signal values for all on/off-line combination for from line center. 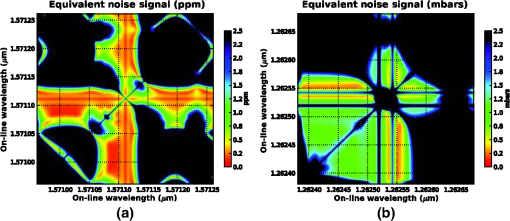 4.ResultsEnsemble sets of simulated signal and noise spectra, centered at 1.5711, 1.5723, and for the bands and at for the band, were created based on a common set of CONUS and globally observed and model atmospheric profile pairs. Simulated signal and noise data were generated for both the reference aircraft and spacecraft configurations described above. In all cases, the path length between the instrument or observer and the surface or target was kept at a constant length to minimize variations in computed values of due to path length variations. All the simulated signal spectra were constructed using the observed or “truth” profile set. In the cases, the nominal profiles at a constant 385 ppm as a function of height were uniformly augmented by fixed amounts at all vertical levels to provide a mechanism for equating signal strength with changes in concentration via linear interpolation. Similarly, simulated signal spectra were constructed by reducing the observed surface pressure. In the case, a fixed value was always subtracted from the observed surface pressure to ensure the resulting calculations were based on the observed data and not subsurface values constructed via extrapolations. Three sets of noise-based optical depth values were constructed for the case based on: (1) the matching NWP model data combined with the observed surface pressure to examine the contributions due to uncertainties in vertical temperature and moisture, (2) the “true” temperature and moisture profiles, plus uncertainties in the observed surface pressure simulated by perturbing the observed by the addition of Gaussian random variable values with and 2 mbar, and (3) the combination of profiles derived from the NWP data and randomly perturbed surface pressure values to examine the total contribution due to uncertainties in atmospheric state knowledge. For only the matching NWP model data combined with the observed surface pressure was used to examine the contributions due to uncertainties in vertical temperature and moisture since the derived quantity is the surface pressure and changes in column should have no impact on observed optical depths in the selected spectral region. These data sets were then used to construct estimates of noise equivalent signal values for optimal sets of on and off-line wavelength pairs over a range from line center for each wavelength range of interest and each noise case described above. The optimal off-line for each selected on-line in this range was computed by locating the minimum noise equivalent signal. This was accomplished by computing the noise equivalent signal for each simulated off-line position in an extended range of from the line center. The minimum noise equivalent signal was defined as the smallest value that fell within a defined off-line region. Off-line selection was limited to regions removed from the line center in order to mitigate line selection near the line center where even though the noise term approaches zero, the signal is most likely below the instrument noise floor. In real-world applications, however, the noise does not approach zero due to other instrument specific and environmental terms not accounted for in this study (such as electronic detector noise). At a minimum, nonzero instrument noise would force the off-line to be selected in a region in which the desired minimum signal thresholds far exceed the transmitter/receiver noise characteristics. In these studies, the off-line values were chosen to be a minimum of , , and from the center line to avoid selection of closely spaced pairs with near zero differences in transmission. Figures 5 and 6 illustrate the results from a sample set of minimum equivalent noise signal analyses. Fig. 5Decomposition of atmospheric uncertainties on optimal performance characteristics. Plots illustrate minimum equivalent noise signal for on-line positions from line center for line at . Plot (a) describes the minimum noise terms for a 5-km nadir viewing geometry, and plot (b) illustrates the results for a 20-km nadir view. Both panels illustrate the minimum equivalent noise associated with uncertainties in vertical temperature/moisture (T/WV) only, a 1-mbar uncertainty in surface pressure with perfect knowledge of temperature/water vapor, and 2-mbar surface pressure uncertainty. The plots show results derived from CONUS NWP data. 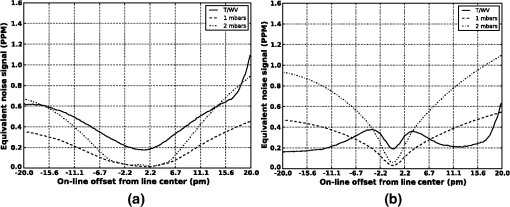 Fig. 6Analysis of impact of uncertainties in vertical temperature and moisture on on-line selection. The plot illustrates the estimated minimum equivalent noise signal for both the 5- and 20-km nadir viewing geometries. The black lines denote the NAM-based results, and the blue represent the results for the GFS-based simulations. 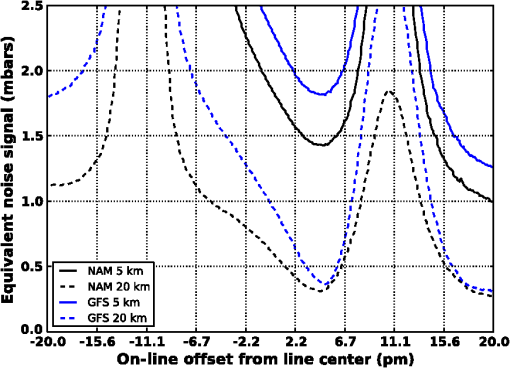 Figure 5 shows the decomposition of several potential noise terms and values for a sample line at . The panels in Fig. 5 illustrate the resulting estimated minimum equivalent noise described as function of measured quantity (equivalent noise signal) for column measurements from 5-km aircraft (a) and from space (b). The solid lines in both define the estimated noise equivalent signal given the combined uncertainties in vertical temperature and water vapor for both the profile sets derived from the global atmospheric state variable sets. In this case, nearly identical results were obtained using the CONUS-based profile data. The dashed and dot-dashed lines illustrate the wavelength dependent noise equivalent signal associated with 1 and 2 mbar unbiased errors in surface pressure knowledge. In this case, the black and the blue line colors denote the underlying input profiles used to construct the observed and modeled optical depths. Both the observed and modeled values were constructed using identical vertical temperature and moisture distributions derived from the observed dataset with varying surface pressures/surface heights. The nominal differences between the equivalent signal derived from the CONUS profile set and those constructed using the global sample sets simply illustrate the variation due to the finite number of samples in each profile set. It is assumed that as the number of samples in each set approaches an appropriately large number, these differences would approach zero. The error terms associated with the aircraft simulations (left-hand panel of Fig. 5) show broad error functions that mimic the underlying absorption feature characteristics with minimums for both variation in temperature and moisture as well as uncertainties in pressure near the line center. The predominant error term in this scenario is due to uncertainties in temperature and moisture over most of the considered bandwidth and is only equivalent to the errors associated with uncertainties in surface pressure at the edges of the band of interest, where the associated weighting functions have significant differences in absorption near the surface. However, for most of the region the noise equivalent signal is dominated by uncertainties in the vertical temperature and moisture. In this case, the simulated errors based on both the CONUS and the global data sets are very similar in magnitude. These similarities are primarily due to nearly identical vertical temperature error characteristics in the 0 to 5-km region and relatively modest contamination due to in-band water vapor features. The most significant contamination due to water vapor occurs on the right-hand side of the figure with on-line wavelengths greater than from the line center. In this scenario, the impact of modest uncertainties in surface pressure knowledge have little impact on the estimated column amount due to both the slowing varying density in along the path and nearly constant absorption along the short path of interest. The same is not true for the simulated satellite case shown in the right-hand panel in Fig. 5. In this case, uncertainties in vertical temperature and moisture dominate in a very narrow region around line center (), and have inflection points on both sides of the line center which correspond to the maximum slope on each side of the underlying absorption feature. In the region beyond from the line center, uncertainties in surface pressure are either of similar magnitude or dominate the budget due to differences in much more well-defined weighting functions that peak nearer to the surface as the on-line moves farther from the line center. Figure 6 illustrates the companion decomposition for the selected band in the region. In this case, only the impact of the atmospheric temperature and moisture is considered since variations in surface pressure represent the signal of interest. The solid lines in the figure describe the average noise equivalent signals associated with the simulated aircraft geometry and those associated with the simulated spacecraft measurements are given by the dashed lines. The black lines in this figure depict the values derived from the CONUS profile set, and blue lines show the results based on the differences in the global profile sets. In this case, the most notable observation is the pronounced differences between both the simulation results based on the CONUS observations and those developed from a global data set. These differences help emphasize the sensitivity of these measurements to uncertainties in atmospheric state knowledge. The aircraft 5-km simulations show a very broad minimum with an optimal value in the range of 0.4 to 0.5 mbar located at from the trough center. The simulated spacecraft optimal noise equivalent signal has much more pronounced error characterization curves with a distinct minima of at from the trough center. These curves roughly follow the trough structure and the representative mean signal and noise values shown in the right-hand panel of Fig. 3. The fact that the minima lie slightly off trough center is due to the fact that the noise associated with uncertainties in vertical temperature and moisture is asymmetric around the trough center as illustrated in Fig. 3. Although the average signal sensitivity is not optimal at this location, the ratio of signal sensitivity to inherent noise is optimal. Figure 7 shows the aggregated wavelength-dependent noise equivalent signals for the three different absorption lines examined in this study. The upper set of plots describes the aggregated optimal noise equivalent signal given uncertainties in vertical atmospheric state and a 1-mbar uncertainty in surface pressure for both the aircraft (left) and space-based (right) simulations. The lower set illustrates the optimal equivalent signals as a function of wavelength offset from the line center associated with simulated atmospheric uncertainties with a 2-mbar variation in surface pressure. The result for all three center wavelengths (1.571111, 1.572335, and ) are plotted in each of the panels by describing the -axis as a pm offset from the line center. The most striking features are the differences in noise equivalent signals computed for the 1.571111 and absorption features and the values for the lines selected around . There is a significant increase in the noise equivalent signal due to uncertainties in vertical temperature and moisture for the line. This is most prevalent near the line center where, in the 5-km aircraft case, the difference is on the order of 0.6 ppm while the spacecraft simulation exhibits a predominant peak at the line center that dominates the cumulative noise term. These results are confirmed by the decomposition of the noise terms due to atmospheric temperature/moisture and uncertainties in surface pressure (not shown for the case) and the difference between the CONUS and global profile. The global profile-based simulations have, in general, larger RMS differences primarily in surface temperature as well as a significant increase in the differences in the lower tropospheric estimates of water vapor content. This near line-center increase in RMSE dominates the 1-mbar case and represents the dominant error term out to from the line center in the 2-mbar case. Fig. 7Minimum equivalent noise signals for lines centered at 1.5711, 1.5723, and given uncertainties in vertical temperature and moisture plus 1-mbar uncertainty in surface pressure for the two plots at the top (a, b), 2 mbar for those on the bottom (c, d). Panel (a) describes the minimum noise terms for a 5-km nadir viewing geometry, and the plots in panel (b) illustrate the results for a 20-km nadir view. 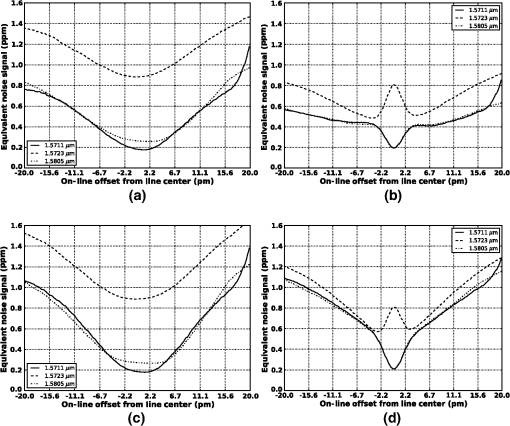 Finally, Tables 1 and 2 provide a tabular form of the estimated optimal noise equivalent signals for a select set of on-line wavelengths and the required off-line position required to achieve the indicated signal-to-noise ratio. Table 1 shows the values for the three spectral regions of interest and the associated values for on-line wavelengths 0, , , and from line center. Table 2 shows the corresponding results for the feature examined in this work. In the case, the on-line wavelengths are defined as 0, , , and from the center of the trough. The optimal values for the case range from to 0.47 ppm, and the optimal values for the selected waveband range from 0.41 to 2.08 mbar. Table 1Optimal off-line wavelengths (optimal off-line offset) and noise signal (equivalent noise signal) for three CO2 centerlines at 1.571111, 1.572335, and 1.580513 μm. Results are shown for candidate on-line wavelengths offset from centerline (on-line offset) by approximately 0, ±1, ±2, ±5, and ±10 pm. Results assume a nominal 20-km path length and uncertainties in T/WV and 1-mbar surface pressure.
Table 2Optimal off-line wavelengths (optimal off-line offset) and noise signal (equivalent noise signal) for sample O2 trough at 1.262531 μm. Results are show for candidate on-line wavelengths offset from trough center (on-line offset) by approximately 0, ±1, ±2, ±5, and ±10 pm. Results assume a nominal 20-km path length and uncertainties in T/WV.
Although the objective of this work was not to address the spectroscopic aspects of line selection, a few points are worth noting regarding the results in Tables 1 and 2 since the optimal on-line will be based on a number of factors besides uncertainties in temperature, pressure, and water vapor. First and foremost, on-line selection is based on an average two-way transmission. Optimally, the nominal two-way transmission at the on-line wavelength should be to best balance the loss of signal power as it travels from the observer to the ground and back again with the magnitude of the signal modulation, i.e., change in transmission given a change in the column concentration. Second, there are a number of atmospheric related effects which vary on a line-by-line basis that include pressure and temperature broadening, shifting of the line due to changes in temperature, as well as the impact of a complex set of strong/weak water vapor lines that also vary within the selected band. Although a particular on-line wavelength for an aircraft measurement may result in the appropriate optical depth, the same on-line wavelength may prove suboptimal from a transmission perspective for the space-based case. Again, the line selection results shown in Tables 1 and 2 are intended to convey the isolated impacts of uncertainties in temperature, pressure, and water vapor on line selection. Third, we do not choose the line center at the center of an absorption feature due to its weighting function with primary absorption in the stratosphere. Since concentration offsets are in parts per million, precise knowledge of the “on-line” wavelength is very important and can have a significant impact on the interpretation of the measured optical depth. This is particularly true for lines selected away from the line center. However, wavelength monitoring is specific to each instrument design. For example, a current airborne instrument5 used the beat frequencies between the three transmitted wavelengths (one on-line and two off-lines on both sides of the feature) and a wavelength reference to compute the “precise wavelength” of each laser to within . As part of this work it was assumed that the transmitted wavelengths would be monitored in flight and this precise measure of the wavelength would be provided as part of the auxiliary instrument data and used in the retrieval process to determine the column values associated with the measured optical depths given at that wavelength. 5.ConclusionsThe study presented in this work provides a framework for assessing the impact of imprecise knowledge of the atmospheric state—vertical temperature/moisture profiles and surface pressure—on retrieval estimates of column and concentrations from differential absorption spectroscopy measurements. This study can assist instrument teams in selecting the optimum IPDA laser wavelengths to minimize the impact of meteorological uncertainties in their and measurements. Although this framework does not address the full end-to-end error budget for a specific instrument, which requires specific knowledge of the instrument design and its error terms, it does provide a systematic method for assessing retrieval errors due to ancillary inputs based on an extensive set of matched sonde-based observations with the collocated NWP model data, and a parametric model of surface pressure uncertainties. The results from this study define the lower bounds associated with the noise equivalent signal for an LAS instrument operating in the region, given both nominal uncertainties in temperature/moisture and a 2-mbar uncertainty in surface pressure. Depending on the line position, the equivalent error ranges from 0.2 to 0.8 ppm. These results demonstrate a tradeoff that can be made in the selection of an on-line position that is a complex function of absolute optical depth and the associated weighting function ( or ). In order for space-based instruments to achieve the desired precision and accuracy of , instrument designs will need to balance instrument noise characteristics, on-line optical depth, and the associated weighting function with impacts of measurement uncertainties due to knowledge of temperature, moisture, and surface pressure. Optimally, the round trip optical depth for any selected line should be approximately unity, which dictates the use of an on-line wavelength that is away from the line center even for weak absorption lines like those in the region. Although the selection of on-line wavelengths offset from the line center, which have associated weighting functions that peak near the surface and better capture information that can be used to constrain near-surface fluxes, more emphasis must be placed on the precision of the required surface pressure estimates. The results also reinforce the need to fully characterize the spectral band of interest including even relatively weak nearby absorption features associated with trace gases, in particular those associated with water vapor that cause contamination due to imperfect knowledge of their associated abundances. The results, while limited to the single-sample region of interest at , demonstrate the impact of uncertainties in vertical temperature/water vapor on on-line wavelengths selected in the trough region, and that it might be advantageous to search for alternative on-line wavelengths that are slightly away from the trough minimum if the increase in desired average absolute optical depth can be accommodated by the design. They also indicate that sensitivity to temperature and contamination due to water vapor may play a significant role in the overall instrument error budget, and unless this is carefully done, the errors associated with the column measurements may exceed the nominal results provided by even the global NWP model data. The framework presented in this work can be extended to explore other bands of interest, e.g., those in the region, and the band in the region, as well as spectroscopic features associated with other trace gases such as . In addition, the approach outlined in this work can be combined with detailed instrument specifications that describe their measurement error characteristics to provide a complete end-to-end error budget of expected instrument performance for both aircraft and space-based missions. This methodology will not only aid in the design of the primary LAS instrument, but also those designed to provide estimates of ancillary information such as surface pressure from total column measurements. AcknowledgmentsThis work has been supported in part by a contract to AER from NASA Langley Research Center as part of the ASCENDS CarbonHawk Experiment Simulator (ACES) project funded under the NASA Earth Science Technology Office, Instrument Incubator Program (order # NNL11AD10T). The authors would like to thank a number of their colleagues at the NASA Langley Research Center: Narasimha Prasad for his hard work and dedication that enabled the ACES program to come to fruition, and F. Wallace Harrison, Syed Ismail, and Michael D. Obland for their continued support and insights that has allowed this work to move forward. Additionally, we would like to thank the anonymous JARS reviewer, whose in depth feedback have significantly strengthened the readability and content of this work. Finally, we would like to acknowledge Atmospheric and Environmental Research, Inc. management for their support of this effort over a number of years. ReferencesR. Imasuet al.,
“Upper-atmospheric CO2 concentration retrieved from thermal infrared spectra observed using GOSAT TANSO-FTS (TIR) sensor,”
Proc. SPIE, 7474 74740K
(2009). http://dx.doi.org/10.1117/12.830387 Google Scholar
A. J. Coganet al.,
“Atmospheric carbon dioxide retrieved from the Greenhouse gases Observing SATellite (GOSAT): comparison with ground-based TCCON observations and GEOS-Chem model calculations,”
J. Geophys. Res.: Atmos., 117
(D21), 2156
–2202
(2012). http://dx.doi.org/10.1029/2012JD018087 JGRDE3 0148-0227 Google Scholar
A. Butzet al.,
“Toward accurate CO2 and CH4 observations from GOSAT,”
Geophys. Res. Lett., 38
(14), L14812
(2011). http://dx.doi.org/10.1029/2011GL047888 GPRLAJ 0094-8276 Google Scholar
D. CrispC. E. MillerP. L. DeCola,
“NASA orbiting carbon observatory: measuring the column averaged carbon dioxide mole fraction from space,”
J. Appl. Remote Sens., 2
(1), 023508
(2008). http://dx.doi.org/10.1117/1.2898457 1931-3195 Google Scholar
J. B. Abshireet al.,
“Pulsed airborne lidar measurements of atmospheric CO2 column absorption,”
Tellus B, 62
(5), 770
–783
(2010). 0280-6509 Google Scholar
J. T. Dobleret al.,
“Atmospheric CO2 column measurements with an airborne intensity-modulated continuous wave 1.57 um fiber laser lidar,”
Appl. Opt., 52
(12), 2874
–2892
(2013). http://dx.doi.org/10.1364/AO.52.002874 APOPAI 0003-6935 Google Scholar
G. D. Spierset al.,
“Atmospheric CO2 measurements with a 2 um airborne laser absorption spectrometer employing coherent detection,”
Appl. Opt., 50
(14), 2098
–2111
(2011). http://dx.doi.org/10.1364/AO.50.002098 APOPAI 0003-6935 Google Scholar
Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond, Washington, DC
(2007). Google Scholar
C. E. Milleret al.,
“Precision requirements for space-based XCO2 data,”
JGR, 112 D10314
(2007). http://dx.doi.org/10.1029/2006JD007659 JGREA2 0148-0227 Google Scholar
S. A. Cloughet al.,
“Atmospheric radiative transfer modeling: a summary of the AER codes,”
Short Commun. J. Quant. Spectrosc. Radiat. Transfer, 91
(2), 233
–244
(2005). http://dx.doi.org/10.1016/j.jqsrt.2004.05.058 JQSRAE 0022-4073 Google Scholar
U.S. DOC/NOAA OFCM, Washington, D.C. Surface Weather Observations and Reports,
(2005) http://www.ofcm.gov/fmh-1/fmh1.htm Google Scholar
E. Rogerset al.,
“The NCEP North American Mesoscale Modeling System: Recent changes and future plans,”
2A.4 Omaha, NE
(2009). Google Scholar
NOAA, Washington, D.C. The GFS Atmospheric Model, NCEP Office Note 422,
(2003) http://www.emc.ncep.noaa.gov/officenotes/newernotes/on422.pdf Google Scholar
B. Sunet al.,
“Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocation on comparison statistics,”
J. Geophys. Res.: Atmos., 115
(D23), D23104
(2010). http://dx.doi.org/10.1029/2010JD014457 JGRDE3 0148-0227 Google Scholar
V. M. Deviet al.,
“Line mixing and speed dependence in CO2 at −1: constrained multispectrum analysis of intensities and line shapes in the band,”
J. Mol. Spectrosc., 245
(1), 52
–80
(2007). http://dx.doi.org/10.1016/j.jms.2007.05.015 JMOSA3 0022-2852 Google Scholar
V. M. Deviet al.,
“Line mixing and speed dependence in CO2 at −1: positions, intensities, and air- and self-broadening derived with constrained multispectrum analysis,”
J. Mol. Spectrosc., 242
(2), 90
–117
(2007). http://dx.doi.org/10.1016/j.jms.2007.02.018 JMOSA3 0022-2852 Google Scholar
L. S. Rothmanet al.,
“The HITRAN 2008 molecular spectroscopic database,”
J. Quant. Spectrosc. Radiat. Transfer, 110
(9–10), 533
–572
(2009). http://dx.doi.org/10.1016/j.jqsrt.2009.02.013 JQSRAE 0022-4073 Google Scholar
C. L. KorbC. Y. Weng,
“Differential absorption lidar technique for measurement of the atmospheric pressure profile,”
Appl. Opt., 22
(23), 3759
–3770
(1983). http://dx.doi.org/10.1364/AO.22.003759 APOPAI 0003-6935 Google Scholar
BiographyT. Scott Zaccheo serves as AER senior vice president of the Technology Solutions Division and the AER chief software engineer for the NOAA/NASA GOES-R Ground System (GS) program. He received his BS in electrical engineering from Lehigh University in 1984, and his MS and PhD degrees in electrical engineering from Tufts University in 1993 and 1995, respectively. He is a member of the ASCENDS science definition team and the NASA LaRC ASCENDS CarbonHawk Experiment Simulator team. Timothy Pernini is a staff scientist at AER. He received his BA degree in physics from Rhode Island College in 2000. His work experience includes analysis of remote sensing data and radiometric calibration of space-based electro-optical sensors. He recently served as AER’s lead systems engineer for implementation of the Solar Ultra Violet Imager and Magnetometer ground processing algorithms for the GOES-R program. Hilary E. Snell serves as AER vice president of the Satellite Programs Division and the AER program manager for the NOAA/NASA GOES-R Ground System (GS) program. He received his AB degree in geophysics from the University of Chicago in 1988, and his MS and PhD degrees in atmospheric and space sciences from the University of Michigan in 1990 and 1994, respectively. In addition to managing the GOES-R program he leads the development of end-to-end remote sensing systems and tailored applications of radiative transfer models. Edward V. Browell is a senior science consultant to the NASA Langley Research Center. He received his PhD degree in aerospace sciences and applied physics from the University of Florida in 1974, and he led the Lidar Applications Group at NASA Langley from 1978 to 2007. He has published over 245 journal papers and written 10 book chapters. He is currently supporting the development of a space-based laser mission to measure the global distribution of . |

