|
|
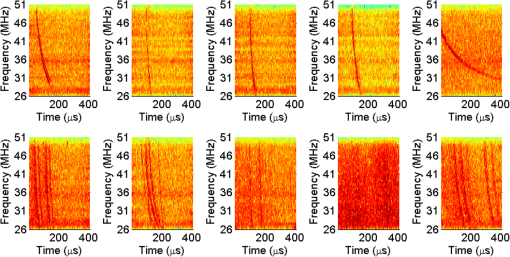
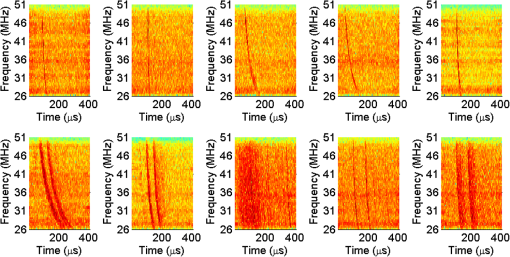
1.IntroductionOngoing research at Los Alamos National Laboratory (LANL) studies the Earth’s radio frequency (RF) background utilizing satellite-based RF observations of terrestrial lightning. The Fast On-orbit Recording of Transient Events (FORTE) satellite provided a rich lightning database that has been used for numerous lightning studies1–3 and some lightning classification work.4,5 In this paper, we explore event classification capability of the FORTE database using adaptive signal processing, combined with compressive sensing and machine learning techniques. We explore two alternative approaches based on nonanalytical dictionaries learned from data using established algorithms and compare them in a classification scenario designed to identify the presence and capture the dynamic behavior of standard lightning event types. A fixed dictionary of parameterized, closed-form elements (e.g., short-time Fourier or a wavelet packet decomposition), whether complete or overcomplete, requires assumptions about the underlying signal sources. The resulting signal representations usually require separate feature selection algorithms, creating additional computational overhead. Also, the representation vector can be very sparse for one category of signal (e.g., constant frequency emitter using a Fourier basis) but dense for another (e.g., chirped pulse using a Fourier basis). Learning dictionaries directly from data remove the closed-form constraint on the dictionary and have led to significant improvements in image processing and computer vision. Several algorithms have been proposed6–9 to learn dictionaries for sparse representation directly from the training data set, and these perform well for both image representation and classification. We previously extended several dictionary learning techniques to simulated RF data10,11 and presented representative classification results for nonstationary, impulsive RF signals in high-clutter, noisy backgrounds. We also extended one dictionary learning method to FORTE data and presented some preliminary results in Ref. 12. In Ref. 13, we showed sparse FORTE feature extraction using analytical overcomplete dictionaries and discussed its potential in conjunction with learned dictionary techniques. We now examine two previously developed supervised dictionary learning methods, the K-SVD algorithm6 and the Hebbian learning algorithm,8 and compare their classification performance on real lightning data using Skretting and Husøy’s minimum residual (MR) classifier, originally introduced for image texture classification.14 We also use subspace analysis based on principal component decomposition in a novel way to illustrate the different ways in which the two dictionary learning methods capture entropy in training data, and to discuss their classification performance. Part of this manuscript was recently published as an SPIE conference proceeding,15 and it is being republished here with some revisions given its potential to significantly impact the classification of remotely sensed time series data. The paper demonstrates possible approaches for established algorithm extensions to nonlinear, nonstationary, and noisy data, even for sensors which are not traditional imaging sensors. More specifically, it provides options for direct feature extraction from data whose underlying analytical model is unknown or of high complexity. Novel to this paper is the classification using a mixed learned dictionary approach to showcase the different ways learning algorithms synthesize information contained in the training data, as well as some pertinent details on software implementation and computational complexity. The layout of the paper is as follows: in Sec. 2, we describe the data environment on-orbit and the characteristics of our data records. In Sec. 3, we summarize the two learning methods we used and the classification scenario and explore classification performance in Sec. 4. We discuss the PCA findings in Sec. 5 and conclude with a brief discussion of future work in Sec. 6. 2.FORTE Satellite DataFor over two decades, LANL programs have included an active research effort utilizing satellite observations of terrestrial lightning to learn more about the Earth’s RF background. One of the richest satellite lightning databases ever recorded is that from the FORTE satellite, developed jointly between LANL and the Sandia National Laboratory under Department of Energy oversight. The FORTE satellite returned years of data from its two types of RF payloads. The LANL FORTE RF database remains relevant for the application of modern event classification techniques, to advance both lightning research in the scientific community and programmatic work to improve future satellite capabilities. 2.1.FORTE SatelliteFORTE was launched on August 29, 1997, into a nearly circular 70-deg inclination orbit at an altitude of 800 km altitude. RF data acquisition commenced within days and continued without serious interruption through 2004. The performance and capabilities of the RF payloads16 as reflected in RF data gathered during the first full year of the FORTE mission (1998) are summarized in Ref. 12. The data reported below are from the narrow-band Twenty (MHz) And Twelve (bit) Receiver (TATR) system, which has two independently tunable passbands, tunable in steps between 20 and 300 MHz. Each passband’s signal is analog filtered to a 22-MHz effective bandwidth and then digitized at 50 megasamples/s. In the data to follow, one of the 22-MHz TATR receivers was placed in the range of 26 to 48 MHz, with a nominal 38-MHz center (low band), and the other in the range of 118 to 140 MHz, with a nominal 130-MHz center (high band). We used low band triggering, as it tends to trigger off the more intense part of the signal spectrum and allows the very high frequency (VHF) signal spectrum to be roughly inferred from the relative power on the two broadband channels. In this paper, we focus on low band measurements and use records including of pretrigger samples, i.e., each recorded time series has 20480 samples. VHF signatures, usually of lightning events, occur in highly nonstationary backgrounds and exhibit both discrete and continuous dynamical behaviors, e.g., trains of chirping pulses combined with continuous time-varying emissions during a single pulse. The generating electromagnetic process may last for a wide range of time scales and usually occurs in the presence of additive white noise and structured clutter, predominantly continuous-wave (CW) and gated-CW sources. The background content has varying levels, and the signal-to-noise and signal-to-clutter ratios can be very poor at times. Depending upon the exact type of lightning (e.g., cloud-to-ground, intra-cloud, etc.), there usually exist some dominant signal features discernible to a subject matter expert, but automatic classification based on time series features is difficult. 2.2.Ionospheric EffectsThere is a distinctive ionospheric dispersion (i.e., nonlinear chirp) that impacts all data records and is particularly noticeable in the low band.17,18 The effect is approximately described by a group delay versus frequency as follows: where is the radio frequency and is the line-of-sight-integrated total electron content (slant TEC). Figure 1 shows an example lightning event time series (left), and its corresponding spectrogram (right), exhibiting multiple transionospheric pulses with mode split and slight dispersion variations. The time-domain signal is prewhitened as described in Sec. 3.3.Fig. 1Low-band zoomed-in example intra-cloud (IC) lightning event time series (a), and its corresponding spectrogram (b), exhibiting multiple transionospheric pulses with varying dispersion. 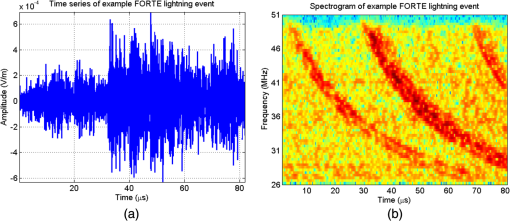 The values of TEC are highly dependent upon the time of day, latitude, and solar weather; they can span a wide range from few units up to a few hundred units. The group delay in Eq. (1) is typical for an ionosphere-refracted signal for higher frequencies (), but the variation with frequency is more complex than for lower frequencies.17 Ultimately, at the lowest frequency supporting a transmission path from the ground to the satellite, the group delay diverges and an exact treatment of the fully anisotropic dispersion relation would be required.2 These rich temporal and frequency characteristics in the VHF signatures recorded on-orbit present challenges for traditional feature extraction and classification approaches, many of which require some form of signal stationarity. Also, while the nonlinear chirps are apparent in the joint time/frequency domain, the computational complexity of sometime/frequency methods renders them impractical for real applications. 2.3.Types of RF EventsThere were several categories of lightning RF events detected by FORTE, and they can be broadly grouped into two classes, cloud-to-ground (CG), and intra-cloud (IC). CG events are most frequent among the FORTE records and generally produce broadband RF emissions that are of longer duration ( of . IC events can include multiple transionospheric broadband pulse pairs of a small time extent (). These pulse pairs consist of an intra-cloud implusive discharge followed by a delayed ground-based reflection of that event. While many of the FORTE IC records contain a single pulse pair, there are a non-negligible number of instances where multiple pulse pairs occur within the same record. In addition, FORTE also recorded signals emitted by the Los Alamos Portable Pulser (LAPP), a research facility for transmitting broadband VHF/UHF single-pulse signals to satellites for the purpose of characterizing those satellites’ radio receivers.19 Although the transmitted signal was linearly polarized, the magnetic anisotropy of the ionospheric dielectric caused the signal to arrive at the satellite as a sum of “fast” and delayed “slow” modes.17 LAPP shots represent a small percentage of total FORTE records (), but are of interest for testing signal processing approaches such as the one detailed in this paper. More example FORTE recordings and spectrograms are shown in Ref. 13. 3.Learned Dictionaries for RF Data3.1.Dictionary Learning AlgorithmsLearning dictionaries from the data can eliminate the need for prior knowledge of possible lightning characteristics and background clutter, while providing sparse representations that perform well in conjunction with a statistical classifier. First, we applied the K-SVD method of Aharon et al.6 to learn features from the FORTE data. The K-SVD algorithm is similar to the -means clustering process, and it works with any form of sparse signal representation algorithm. Secondly, we used Hebbian learning10 to build dictionaries from the same training data and used the MR classifier to compare the performance of the two dictionary learning methods. The MR classifier was introduced for image texture classification in Ref. 14 and is conceptually the same as the nearest subspace classifier.20 We have successfully applied it to classification of simulated RF data10 and begun extending it to FORTE-related work.12,13 We now briefly describe the dictionary learning algorithms as found in image processing literature. Given a signal class containing normalized training vectors , each of length , the dictionary learning begins by initializing the elements of the dictionary with normalized data vectors randomly extracted from the training set (i.e., imprinting). Other possible dictionary initialization methods include seeding with random unit-norm vectors or with a sparsifying transform of the training data. Learning Φ takes place over multiple iterations (the number of times the dictionary “sees” the entire training data set) and generally consists of two stages per learning iteration. In the “sparse coding stage,” which is the same for both K-SVD and Hebbian learning, we seek a weight vector for each training vector such that is sparse and is a sufficiently good approximation of the input where the sparsity factor, , controls how many dictionary elements are allowed to represent a particular training vector. Computationally, this problem is NP-hard, lacking an exact solution, but we can find an approximate solution for using a simple matching pursuit algorithm.21 Other approaches to forming good approximate sparse representations, such as orthogonal matching pursuit22 or an basis pursuit,23 can also be used, but they lead to higher computational demands.For K-SVD learning, once we find a sparse matrix of weight vectors, , over the current dictionary iteration for all training data, we proceed to the “dictionary update stage.” In the K-SVD case, the training vectors are viewed simultaneously by the dictionary, and each dictionary element is sequentially updated based on the group of training vectors it helps to represent, as shown in Ref. 6 and summarized below. Let Here the matrix is the signal residual after the contribution of all dictionary elements different from is subtracted. The residual matrix is then restricted to rows that represent the residual for the training vectors that contain in their sparse representation. Given the singular value decomposition the dictionary update rule is , where is the largest singular vector. K-SVD also uses a back-projective algorithm to update the dictionary weights in order to improve the approximations of the matching pursuit.In the Hebbian learning case, we perform an update of the entire dictionary for each training vector using the learning rule where is a constant parameter controlling the learning rate, and the new estimate is renormalized to the unit norm. That is, in each learning iteration, the dictionary is updated as many times as there are training vectors, . The training vectors are received in a random order which changes at each learning iteration. The Hebbian dictionary update,, is derived to minimize the energy cost function for sparse representation of the input vector8 given byThe first term measures how well the dictionary describes the training vector , according to mean square error, whereas the second term enforces sparsity in the weight vector . The dictionary update is obtained by performing gradient descent on this cost functional, resulting in The learning iterations, each with a sparse coding and an update stage, continue until some criterion is fulfilled. This criterion can be a measure of dictionary convergence (i.e., the individual dictionary elements stop changing significantly between consecutive updates), a measure of representative or discriminative power, or an empirically chosen fixed number of learning iterations. In this paper, we consider a range of in order to explore dictionary convergence as a function of learning iterations, with a fixed learning sparsity factor , and a varying classification sparsity factor, . 3.2.Dictionary Size and Data WindowingIn previous work, we used small data windows (e.g., 1024 samples or ) extracted from the full sample-length record to test localized feature extraction both via machine learning techniques,12 as well as via overcomplete analytical dictionaries of chirplets.13 We sought to automatically determine whether the data window contained any broadband signal or chirping component, and then used the window-level classification in a hierarchical, dynamic process analysis for large time-scale classification. However, the distribution of broadband features in a full lightning record can vary significantly, making this a nontrivial problem. In this paper, we consider much longer data windows, specifically 10,240 and 20,480 samples long, that is, we consider either each of pretrigger and posttrigger samples, or the entire record. The dictionary size, , is a parameter that needs to be set and is usually chosen based on the size of the data windows, and on the subjective assessment of intrinsic data dimensionality. Here, we learn dictionaries of sizes and elements, respectively, and focus our analysis only on the low band records. 3.3.Data PreprocessingReducing the background clutter prior to dictionary learning is an important preprocessing step. Each full record is prewhitened to suppress CW carriers (i.e., narrow-band signals) in the frequency domain. Frequency components with the most power are, therefore, rescaled so their average power clamps at a value just above the overall record noise, as shown in Ref. 12. Preprocessing can also involve ionospheric dispersion correction or dechirping. The value of S in Eq. (1) can be coarsely derived by optimally aligning the spectrogram into vertical features, i.e., finding the inverse slant TEC value that best “dechirps” the impulses. This dechirping step is not applied in the work described in this paper and will be the topic of future investigation. 3.4.Training DataWe learn from prewhitened training data, using FORTE low band recordings from the entire year 1998. While the FORTE dataset is extremely rich in the number and types of RF events it captures and the phenomenology it reveals, the existing human-verified databases of single-class lightning events are limited in size. That is, there are no training sets of sufficiently large size for robust feature extraction (at least a few thousand records) and with verified ground-truth labels for the types of lightning we wish to classify. Previously in Ref. 12, we attempted to build a universal Hebbian dictionary that learned from all classes and had to be used in conjunction with a statistical unsupervised classifier (i.e., -means). We also implemented a LAPP versus non-LAPP classification scheme,13 using Hebbian dictionaries learned from short data windows. We use the LAPP and non-LAPP training data sets again to learn longer time duration dictionaries and to compare two different established learning methods. We extract 823 LAPP records from the entire 1998 FORTE database based on timestamp information and visually verify each to be a true LAPP shot. We also compile a non-LAPP database of equal size (823 records) containing CGs and ICs in the relative usual proportions (i.e., dominant CGs). The full records are prewhitened prior to learning, and the majority of background clutter is thus removed. For this two-class problem, we learn dictionaries in pairs, one LAPP and one non-LAPP, for each learning method and for every parameter setting we consider in this paper. 3.5.Learned FeaturesOne way to visualize what the dictionary learns is to look at spectrograms of the dictionary elements at the same equivalent sampling frequency of 50 MHz. Shown below are spectrograms of example elements from dictionaries of size , learned using the K-SVD algorithm (Fig. 2) and the Hebbian algorithm (Fig. 3). The top panel in each figure shows elements from the LAPP dictionary, and the bottom panel shows elements from the paired non-LAPP dictionary. The CW components are barely discernible in the elements due to the data prewhitening, and we see defined chirping components in both dictionaries, either LAPP-like, or lightning-like. In some cases, the elements capture the mode split due to ionospheric birefringence imposed by the geomagnetic field. It is important to note that visually there is no significant distinction in the spectral domain between the selected K-SVD and Hebbian dictionary elements. 4.Classification using Learned DictionariesTo classify a test time series from equally sized LAPP and non-LAPP data sets, we represent it individually over the dictionary pair via matching pursuit, yielding two sparse representations, as detailed in Ref. 12. The energy compacting property of matching pursuit is used for this specific application using MR classification with very sparse approximation. The MR classifier assigns the label corresponding to the dictionary yielding the smallest matching pursuit residual energy to each test window. That is, the MR classifier decides based on the best matched space, or the “nearest” dictionary space to the test data. The classification labels for test data are compared with the ground truth labels to obtain classification accuracy, which is used as the performance metric throughout this paper. We compare the K-SVD and Hebbian methods in terms of their classification performance on LAPP versus non-LAPP equal-sized test data as a function of the number of learning iterations, , number of dictionary elements, , and approximation sparsity in the classification stage, . In reporting accuracy, we assume that false positives (false LAPPs) and false negatives (false non-LAPPs) are equally weighted; however, for applications in which false positives and false negatives are not assigned equal weight, the data from which the dictionary is learned could be chosen to minimize either the false positive rate or false negative rate. These classification labels were compared with the true labels in the usual classification metrics of “accuracy” [], “recall” [], and “specificity” []. For ease of visualization, LAPP dictionaries will be marked on the plots below as ON and non-LAPP dictionaries as OFF. We first consider the straightforward case of using each type of dictionary separately, that is, both ON and OFF dictionaries in a classification test are of the same type, Hebbian or K-SVD. Figure 4 summarizes the mean classification performance (averaged over the number of dictionary learning iterations, ), for 10240-sample length data windows and number of dictionary elements [(a) column], and for 20480-sample length data windows and number of dictionary elements [(b) column]. Classification metrics (-axis) are shown as a function of classification sparsity factor, , for both Hebbian (green traces) and K-SVD (blue traces) learning algorithms. As far as the effect of classification sparsity factor on performance, plots show the MR classifier performs best in the case of very coarse approximation, i.e., after just one to two dictionary elements in approximation, similar to our findings in Ref. 10. As the approximation becomes finer (more elements are added), the impact on performance is, at best, negligible. Numerically, classification accuracy is slightly higher than the range determined by Ref. 4, however, a direct comparison of performance is not possible due to the marked differences in classification scenarios, algorithm, and training data. Fig. 4Mean classification performance (averaged over number of learning iterations, C), for 10240-sample length windows and dictionary elements (left column), and for 20480-sample length data windows and dictionary elements (right column). Classification metrics (-axis) are shown as a function of classification sparsity factor, Lclass for both Hebbian (green traces) and K-SVD (blue traces) learning algorithms. 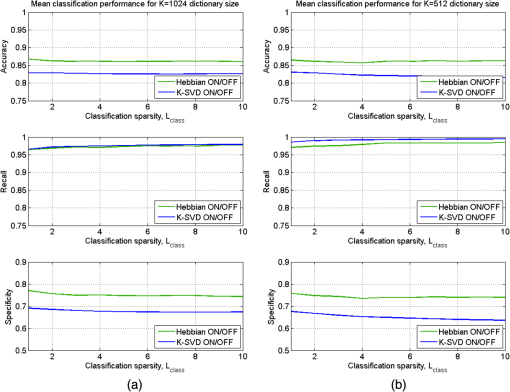 Classification accuracy (top panel) is very similar between the two dictionary sizes, with a consistently higher mean performance given by Hebbian learning compared to K-SVD, although not by much. The recall rates (middle panel), that is, the rate of correctly identifying LAPP shots, is relatively high for both methods, with better results achieved in the smaller dictionary case (i.e., full-record learning case). Specificity (bottom panel), or performance in recognizing non-LAPP events, is much poorer than recall, especially for the K-SVD case. The plots indicate that for data that is self-similar (LAPP data), the two methods perform very similarly. For widely varying data (non-LAPP), the methods appear to perform quite differently. Secondly, given the different ways the two methods appear to extract discriminative features from the training data, we consider the case of mixing the two types of learned dictionaries in classification. We run the full MR classification test corresponding to Fig. 4 both for the combination {Hebbian ON, K-SVD OFF} and for the combination {K-SVD ON, Hebbian OFF}. The corresponding performances (averaged over a number of dictionary learning iterations, ) for each of the three classification metrics are summarized in Fig. 5, for 10240-sample length data windows and number of dictionary elements (left column), and for 20480-sample length data windows and number of dictionary elements (right column). Figure 4 suggested that Hebbian dictionaries give better fits for non-LAPP data (i.e., their specificity was higher), so the expectation is that a {K-SVD ON, Hebbian OFF} combination would lead to better results in the mixed dictionary case compared to its counterpart combination. This is indeed the case in Fig. 5, where the blue trace corresponding to the {K-SVD ON, Hebbian OFF} combination reaches a higher accuracy for both dictionary sizes (top panel), higher specificity (bottom panel), and a negligible decrease in recall rate (middle panel). Fig. 5Mean classification performance (averaged over number of learning iterations, C) as a function of classification sparsity factor, Lclass. Classification uses mixed dictionary types for 10240-sample length windows and dictionary elements (left column), and for 20480-sample length data windows and dictionary elements (right column).  The mixed dictionary approach introduced here illustrates how a user could take advantage of the strengths of various learning techniques and tailor them to fit the particular real data application. Section 5 explores in a little more detail the learning differences between the two methods evaluated in this paper for FORTE data. 4.1.Aspects of Algorithm Implementation and Software ComplexityA practical challenge for RF signal processing is the length of the time records, the high-data rate, and the equivalent short processing time available for real-life applications. For learned dictionary methods, the two separate algorithm components that need to be optimized are the “learning stage” and the “classification stage.” Learning a dictionary of size can be computationally very expensive, depending on number of dictionary elements, length of elements (i.e., size of data window), and amount of training data. Since we use supervised learning, and in our case do not update the dictionary with every new test set, the learning stage becomes upfront computational overhead and can, in theory, be reduced by use of parallel computing hardware wherever possible. At a particular sequential update iteration, we can scatter the inner products between data and dictionary elements across multiple cores, resulting in complexity, where is the sparsity factor, is the length of a dictionary element, and is the number of training data windows. For the K-SVD algorithm, the SVD decomposition in the dictionary update step is the computational bottleneck, as it can take up to element update at every learning iteration for our given training set size, using a 64-bit Win7 machine with multiple Xeon X5550 processors. For example, a single learning iteration (i.e., a full cycle of ) for a K-SVD dictionary with 1024 elements of length 10240 takes 3904.14 s on average and takes 1145.93 s on average for a K-SVD dictionary with 512 elements of length 20480. The Hebbian update is much faster and grows linearly with the length of the dictionary element (or size of data windows), as shown in Eq. (7). The classification of test data is done using a vectorized implementation. Unlike over-complete dictionaries, whose number of elements can be larger by an order of magnitude compared to the length of the data, , our learned dictionaries are undercomplete, i.e., , which leads to an increase in classification speed. At each matching pursuit iteration, the calculation of the inner products between a data window of size and the dictionary elements can be scattered across multiple cores, reducing the complexity to , where is the sample length of a time series. The most significant speedup in the matching pursuit stage was obtained by buffering the test data (i.e., passing the data to the classifier in a vectorized format of windows on length samples) and using logical software masks to facilitate simultaneous sparse adaptive decomposition of the data. Additional speedups can, in theory, be achieved by distributing some of the calculation across the cores of a graphical processor unit, and this will be investigated in future work. 5.Learned Dictionary SubspaceAs Eqs. (2–7) indicate, the two dictionary learning methods extract information from the training data in different ways. On one hand, Hebbian learning fine-tunes relevant dictionary elements based on each individual training sample, or each small batch of training samples if run in an on-line batch mode. In other words, we can refer to Hebbian learning as defined in Sec. 3.1 as having a short-term memory. One advantage of such memory is that the resulting dictionary has a good chance of capturing relevant features for some of the training data at a particular instance. This suggests that for datasets with high intrasample variation, Hebbian learning may be more adept at capturing the high-fidelity features. The downside is the risk of converging to local minima. Our previous experience implementing Hebbian learning indicates the number of learning iterations needed to achieve consistent classification accuracy performance must be adequately large.11 On the other hand, K-SVD updates the dictionary elements using the most dominant feature from the training set seen as a whole, or in a very large batch. That is, from a large group of training samples, only the information contained in the associated first singular vector is captured by the dictionary. This type of learning indicates the method’s memory is global, rather than local, and it results in the dictionary converging to average features in fewer iterations compared to Hebbian learning. K-SVD dictionaries may, therefore, perform very well on data sets that have a high-degree of self-similarity, since that self-similarity would be well captured by the SVD-based update. For data sets that have a high degree of intrasample variation, K-SVD is not explicitly designed to retain the high-fidelity features, and it will likely lead to a decrease in classification performance, as seen in Sec. 4. Training data are all sampled from the same data space, i.e., from the same data distribution. It is this very data space that the proposed dictionary learning methods are aiming to learn from the training data. The training set, therefore, must include sufficient information (i.e., entropy) to adequately describe the entire data space. A way to assess the data space is to perform principal component analysis (PCA) on the matrix formed with all the training vectors and to evaluate the space spanned by the resulting principal vectors. We similarly apply PCA on example dictionaries learned with the two methods, K-SVD and Hebbian. The outcome of principal component decomposition is most typically described in terms of variation captured by the eigenvectors, that is, the cumulative sum of the ordered eigenvalues. A second way to describe PCA outcome, much less typical and somewhat subjective, is using principal component biplots. We will use both approaches to gain more insight into our data and dictionary spaces. Plots of the eigenvalues corresponding to the principal component decomposition are shown in Fig. 6 for the LAPP training data (left), and non-LAPP training data (right), for training sets (red trace), K-SVD dictionary (blue trace), and Hebbian dictionary (green trace). We see that the training data needs principal components to account for of the variance; this high number is indicative of very high data entropy, as expected for this data set. By contrast, both dictionary learning methods need almost twice that number of principal components to capture a similar degree of variance, and their respective cumulative eigenvalue sums have similar growth rates. This could be an indication that the learned dictionaries, shown in Fig. 6, have room for improvement in representing the training data space. Fig. 6Cumulative sum of eigenvalues for LAPP learned dictionaries (a), and non-LAPP learned dictionaries (b) with elements. Green trace corresponds to Hebbian dictionaries, and blue trace corresponds to K-SVD dictionaries; training data set eigenvalue cumulative sum is shown in red. 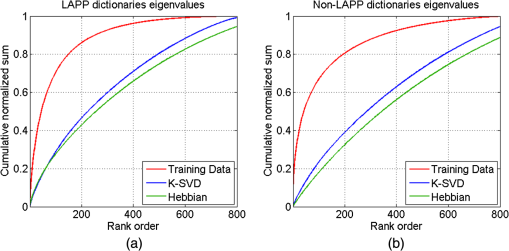 Figure 7 shows biplots of the LAPP training data (left) and non-LAPP training data (right). The biplots allow visualization of the magnitude and sign of each training input’s contribution to the largest two principal components and also show each input represented in terms of those two components. The axes in the biplot represent the magnitudes of the first two largest principal components, with variables (i.e., the 10240 samples in a time series) represented as blue vectors. The vector direction and length indicate how the variable contributes to the two principal components in the biplot. Each of the training inputs is represented by a red dot, and their locations indicate the score of each observation for the two principal components. The cosine of the angle between any two vectors approximates their degree of correlation, and the vector lengths approximate the standard deviations of the corresponding variable. The Euclidian distance on a biplot between two observations (red dots) approximates their standardized distance, that is, the squared root of the Mahalanobis distance.24 Fig. 7PCA biplots for the LAPP training set (a), and non-LAPP training set (b) for 10240-sample length data windows. 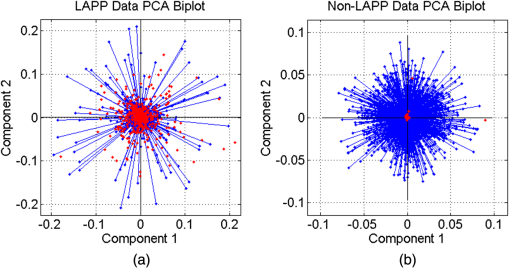 The biplots in Fig. 8 correspond to dictionary PCA and similarly show the magnitude and sign of each dictionary element’s contribution to the largest two principal components. The figure axes are kept identical to the respective axes in Fig. 7 to facilitate comparison of the LAPP versus non-LAPP case. A visual analysis of the biplots indicates that the two dictionary learning methods seem to capture the training data information in different ways, as evidenced both by the different shape of the radial dependence of dictionary samples with respect to the first two principal components (i.e., relative lengths of the vectors), as well as by the respective distribution of the scores. A more direct comparison of actual vector lengths in the biplots is difficult, largely due to the matrix-specific PCA variable scaling. In the LAPP data case, Hebbian learning appears to lead to dictionary elements more similar to the training data, whereas in the non-LAPP case, the K-SVD dictionary appears more similar to the training set. This can possibly be explained by considering (a) the respective degree of similarity in the two training datasets (i.e., LAPP events are highly repeatable or self-similar, whereas the non-LAPP lightning events are very different one from another) and (b) the type of dictionary updates over the training set (i.e., sequential, or with “short memory” in the Hebbian case versus aggregated, or with global memory in the K-SVD case). Fig. 8PCA biplots for example K-SVD dictionaries (top row), and example Hebbian dictionaries (bottom row), learned from the LAPP training set (left column), and non-LAPP training set (right column) for 10240-sample length data windows. 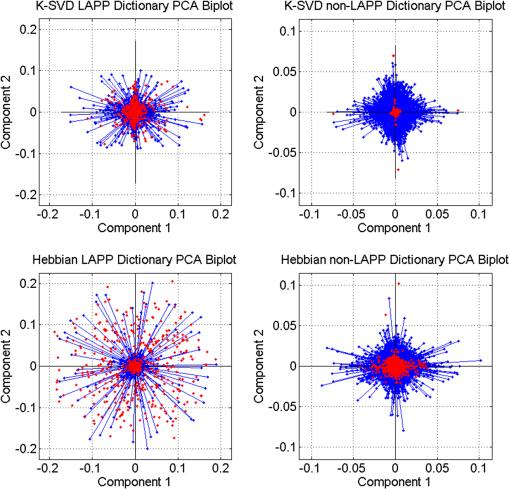 The PCA indicates that there is a high degree of variability present in both LAPP and non-LAPP training data sets, as expected, and the underlying data spaces may be quite large in dimensionality. Compounded with the analysis of the learned dictionaries, it suggests that larger dictionary sizes might be needed for time-domain analysis than those studied in this paper to adequately capture the variability in the training data space. 6.ConclusionThis paper extends two established dictionary learning techniques to satellite RF lightning classification using FORTE recordings. We highlight the many challenges offered by this real RF dataset and present preliminary comparative results for a reduced set of dictionary learning parameters and data preprocessing options. We apply domain expertise to extract adequately sized labeled training sets to learn dictionaries specific to individual RF event classes. We use a two-class scenario designed to distinguish between LAPP shots and real lightning events, suggesting that event-specific dictionaries of sufficiently large size could be used for discrimination using a nearest subspace classifier. We evaluate classification performance as a metric to quantitatively compare the two learning methods for our application and illustrate performance improvement using a novel mixed dictionary type approach. We also provide a subjective interpretation of principal component decomposition to help guide the research efforts toward parameters leading to meaningful future learning. While this comparative study did not conclusively establish one method’s superiority compared to the other for the specific problem and data set under consideration, it nonetheless suggests that dictionary learning techniques are suitable for real RF data processing and classification. Additional sensitivity studies of the method parameters would be needed both to improve upon each individual method’s classification performance and to enable further comparison. AcknowledgmentsThis work was sponsored by the Department of Energy / National Nuclear Security Administration. ReferencesA. R. JacobsonX. M. Shao,
“On-orbit direction finding of lightning radio frequency emissions recorded by the FORTE satellite,”
Radio Sci., 37
(4), 17-1–17-20
(2002). http://dx.doi.org/10.1029/2001RS002510 RASCAD 0048-6604 Google Scholar
R. W. MosesA. R. Jacobson,
“Ionospheric profiling through radio-frequency signals recorded by the FORTE satellite, with comparison to the International Reference Ionosphere,”
Adv. Space Res., 34
(9), 2096
–2103
(2004). http://dx.doi.org/10.1016/j.asr.2004.02.018 ASRSDW 0273-1177 Google Scholar
X. M. ShaoA. R. Jacobson,
“Polarization observations of lightning-produced VHF emissions by the FORTE satellite,”
J. Geophys. Res.-Atmos., 107
(D20), ACL 7-1–ACL 7-16
(2002). http://dx.doi.org/10.1029/2001JD001018 JGRDE3 0148-0227 Google Scholar
D. Eadset al.,
“Genetic algorithms and support vector machines for time series classification,”
Proc. SPIE, 4787 74
–85
(2002). http://dx.doi.org/10.1117/12.453526 Google Scholar
T. E. L. LightA. R. Jacobson,
“Characteristics of impulsive VHF lightning signals observed by the FORTE satellite,”
J. Geophys. Res.-Atmos., 107
(D24), 4756
(2002). http://dx.doi.org/10.1029/2001JD001585 JGRDE3 0148-0227 Google Scholar
M. AharonM. EladA. Bruckstein,
“K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation,”
IEEE Trans. Signal Process., 54
(11), 4311
–4322
(2006). http://dx.doi.org/10.1109/TSP.2006.881199 ITPRED 1053-587X Google Scholar
J. Mairalet al.,
“Discriminative learned dictionaries for local image analysis,”
in IEEE Conf. Computer Vision and Pattern Recognition,
2415
–2422
(2008). Google Scholar
B. A. OlshausenD. J. Field,
“Sparse coding with an overcomplete basis set: A strategy employed by V1?,”
Vision Res., 37
(23), 3311
–3325
(1997). http://dx.doi.org/10.1016/S0042-6989(97)00169-7 VISRAM 0042-6989 Google Scholar
K. EnganS. O. AaseJ. H. Husoy,
“Method of optimal directions for frame design,”
in Proc. IEEE Int. Conf. Acoustics, Speech, and Signal Processing,
2443
–2446
(1999). Google Scholar
D. I. Moodyet al.,
“Sparse classification of RF transients using chirplets and learned dictionaries,”
in IEEE Asilomar Conf. Signals, Systems, and Computers,
1888
–1892
(2011). Google Scholar
D. I. Moodyet al.,
“Radio frequency (RF) transient classification using sparse representations over learned dictionaries,”
Proc. SPIE, 8138 81381S
(2011). http://dx.doi.org/10.1117/12.898894 PSISDG 0277-786X Google Scholar
D. I. Moodyet al.,
“Adaptive sparse signal processing of on-orbit lightning data using learned dictionaries,”
Proc. SPIE, 8750 87500H
(2013). http://dx.doi.org/10.1117/12.2016160 PSISDG 0277-786X Google Scholar
D. I. Moodyet al.,
“Signal classification of satellite-based recordings of radiofrequency (RF) transients using data-adaptive dictionaries,”
in IEEE Asilomar Conf. Signals, Systems, and Computers,
(2013). Google Scholar
K. SkrettingJ. H. Husøy,
“Texture classification using sparse frame-based representations,”
EURASIP J. Appl. Signal Process., 2006 1
–11
(2006). http://dx.doi.org/10.1155/ASP/2006/52561 1110-8657 Google Scholar
D. I. MoodyD. A. Smith,
“Adaptive sparse signal processing of satellite-based radiofrequency (RF) recordings of lightning events,”
Proc. SPIE, 9124 91240E
(2014). http://dx.doi.org/10.1117/12.2049844 PSISDG 0277-786X Google Scholar
D. C. EnemarkM. E. Shipley,
“The FORTE receiver and sub-band triggering unit,”
in 8th Annual American Institute of Aeronautics and Astronautics (AIAA)/Utah State University (USU) Conf. Small Satellites,
(1994). Google Scholar
R. A. Roussel-DupreA. R. JacobsonL. A. Triplett,
“Analysis of FORTE data to extract ionospheric parameters,”
Radio Sci., 36
(6), 1615
–1630
(2001). http://dx.doi.org/10.1029/2000RS002587 RASCAD 0048-6604 Google Scholar
A. R. Jacobsonet al.,
“FORTE radio-frequency observations of lightning strokes detected hy the National Lightning Detection Network,”
J. Geophys. Res.-Atmos., 105
(D12), 15653
–15662
(2000). http://dx.doi.org/10.1029/2000JD900103 JGRDE3 0148-0227 Google Scholar
D. N. HoldenC. P. MunsonJ. C. Devenport,
“Satellite-observations of transionospheric pulse pairs,”
Geophys. Res. Lett., 22
(8), 889
–892
(1995). http://dx.doi.org/10.1029/95GL00432 GPRLAJ 0094-8276 Google Scholar
J. Wrightet al.,
“Robust face recognition via sparse representation,”
IEEE Trans. Pattern Anal. Mach. Intell., 31
(2), 210
–227
(2009). http://dx.doi.org/10.1109/TPAMI.2008.79 ITPIDJ 0162-8828 Google Scholar
S. G. MallatZ. Zhifeng,
“Matching pursuits with time-frequency dictionaries,”
IEEE Trans. Signal Process., 41
(12), 3397
–3415
(1993). http://dx.doi.org/10.1109/78.258082 ITPRED 1053-587X Google Scholar
S. G. Mallat, A Wavelet Tour of Signal Processing. The Sparse Way, Academic Press, Burlington, Massachusetts
(2009). Google Scholar
S. S. ChenD.L. DonohoM.A. Saunders,
“Atomic decomposition by basis pursuit,”
SIAM Rev., 43
(1), 129
–159
(2001). http://dx.doi.org/10.1137/S003614450037906X SIREAD 0036-1445 Google Scholar
K. R. Gabriel,
“Biplot graphic display of matrices with application to principal component analysis,”
Biometrika, 58
(3), 453
(1971). http://dx.doi.org/10.1093/biomet/58.3.453 BIOKAX 0006-3444 Google Scholar
BiographyDaniela I. Moody is a scientist on the Machine Learning and Data Exploitation Team in LANL’s Data Space Systems Group. She received her PhD in electrical engineering from the University of Maryland, College Park, in 2012 and has been at LANL since 2006. Her current work focuses on developing improved feature extraction algorithms that combine adaptive signal processing with compressive sensing and machine learning techniques. Dave A. Smith is a research and development engineer in the Space and Remote Sensing Group (ISR-2) at Los Alamos National Laboratory. He received his PhD in electrical engineering from the University of Colorado, Boulder, in 1998. He has worked at LANL since 1989. He currently leads a space instrumentation development project. |