|
|
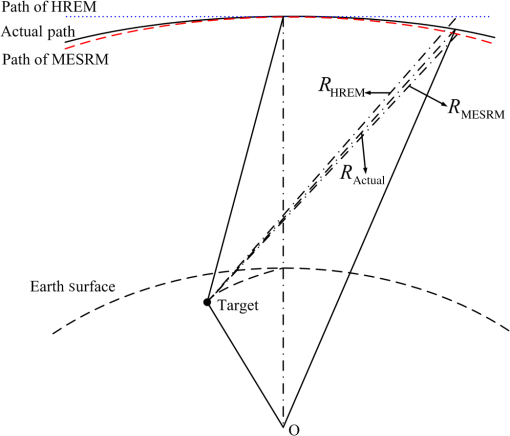
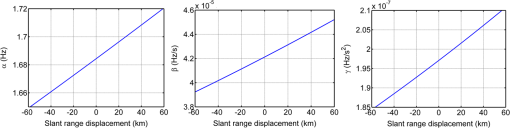
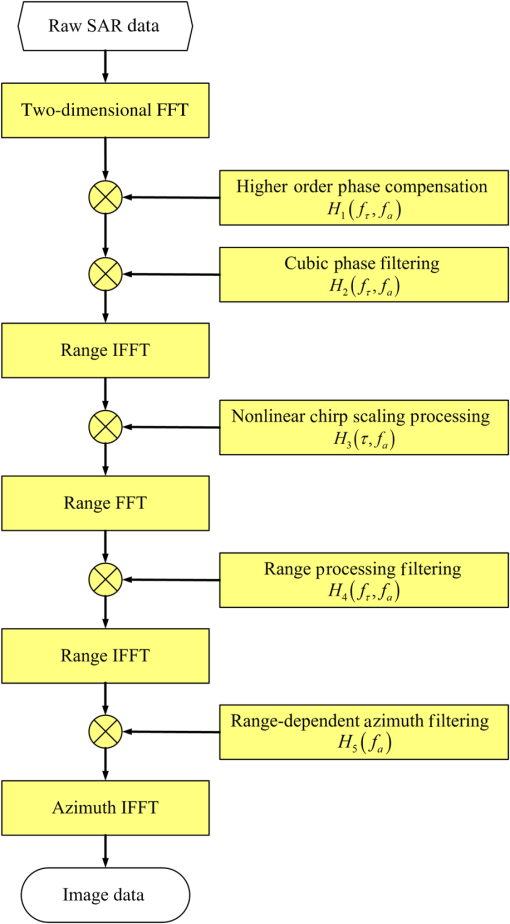
1.IntroductionSynthetic aperture radar (SAR) is a well-established remote sensing technique, capable of acquiring images of Earth’s surface independent of weather conditions and sunlight illumination.1 Since SEASAT was launched in 1978,2 spaceborne SAR has received much attention for its capabilities of Earth observation and environment monitoring. So far, most existing spaceborne SAR systems operate at the low Earth orbit (LEO) near or below 800 km.3 Because of their orbit height, the limitations of LEO-SAR are obvious, such as a long revisit period and narrow mapping swath. Compared with LEO SAR, the medium Earth orbit (MEO) SAR has better accessibility and greater coverage.4,5 However, along with the ascension of the orbit, the relative Satellite-Earth geometry of the MEO SAR will significantly deviate from a straight line, which poses many challenges for spaceborne SAR signal processing, particularly the imaging part. An accurate range model and efficient imaging algorithm are the basis of MEO SAR signal processing. The most well-known range model in spaceborne SAR is the hyperbolic range equation model (HREM),6,7 which is derived from the straight track and is adapted to the curved orbit of spaceborne SAR by equivalent velocity and squint angle. However, for MEO SAR systems, the much longer integration time will introduce significant phase errors in signal processing based on old range models. Eldhuset8,9 proposed a fourth-order Doppler range model (DRM4) to describe the range history of high-resolution spaceborne SAR, where the third- and fourth-order phase errors can be fully compensated and a better imaging result can be obtained. However, the model does not consider the effect of higher order phase errors, which limits its application in MEO SAR. An advanced HREM for MEO SAR was proposed by Huang et al.,10 where an additional linear term is introduced into the conventional HREM so that it can handle the focusing issue of an azimuth resolution around 3 m at altitudes ranging from 1000 to 10,000 km. However, for higher altitudes, its performance degrades dramatically. The method of series reversion is another range model for spaceborne SAR imaging,11 where the range equation is expressed by a series expansion, and its accuracy is dependent on the number of terms used. To meet the requirements of MEO SAR imaging, more than four terms are needed in the expansion, which results in a high-complexity system. In this paper, a modified equivalent squint range model (MESRM), which was employed in our work in Ref. 12, is used as the range model for MEO SAR. The chirp scaling (CS) algorithm is a common approach adopted for the processing of spaceborne SAR data due to its good phase preservation and high efficiency properties.13 However, the traditional CS algorithm was derived based on HREM and cannot be directly applied to our MESRM. In this work, we derive the point target spectrum (PTS) of the MESRM-based signal, and develop an improved higher order nonlinear chirp scaling (NLCS) algorithm for MEO SAR imaging where the improved CS processing is applied to remove the range dependence of a two-dimensional (2-D) point target reference spectrum (PTRS), and the higher order phase compensation, range-matched filter, and range-dependent azimuth filter are used to realize accurate focusing. Extensive simulations are performed to show the significantly improved imaging result. This paper is organized as follows: with a brief description of the MESRM, the PTRS based on MESRM is derived in Sec. 2. The corresponding improved algorithm for MEO SAR is developed in Sec. 3. Simulation results are provided in Sec. 4, and conclusions are drawn in Sec. 5. 2.Signal Model for Medium Earth Orbit Synthetic Aperture Radar2.1.Range ModelThe spaceborne SAR geometry in Earth-centered rotating coordinates is illustrated in Fig. 1, where the actual path is represented by the black solid line, and the paths based on HREM and MESRM are denoted by the blue dotted line and red dashed lines, respectively. For a short integration time, the straight path approximation is sufficient in the LEO cases. However, for the MEO SAR, the straight path approximation cannot properly fit the actual path and another degree of freedom should be used to make the range model more accurate. To improve the precision of the range model, an additional cubic component and quartic component are introduced in the range equation,12 as shown below: where is the azimuth time, is the slant range at Doppler center time, is the equivalent velocity between the scatterer and the SAR, is the equivalent squint angle, is the signal wavelength, and , , and denote the Doppler centroid frequency, the azimuth FM rate, the rate of the azimuth FM rate and the second-order derivative of the azimuth FM rate, respectively, given by where , , , and denote the position vector, velocity vector, acceleration vector, and the rate of the acceleration vector and its second-order derivative, respectively. The subscript sat represents the satellite, and tar represents the ground target. Compared with the traditional range model, the MESRM not only perfectly compensates the actual range history up to the quartic term, but also partially compensates the higher order terms, which makes MESRM more suitable for MEO SAR.2.2.Signal ModelBased on the MESRM, after demodulation to baseband, the received signal for a point target can be described as where represents the scattering coefficient, and denote antenna pattern functions in the range and azimuth directions, respectively, is the speed of light, is the range chirp rate, is the fast time, and is the Doppler center time of point target.In order to obtain the 2-D PTS of the above echo expression, the principle of stationary phase and Fourier transformation (FT) is applied. The 2-D PTS of the echo signal can be obtained as where is the range frequency, is the azimuth frequency, and is the stationary point obtained by solving the following equation:Considering the complexity of the range model, it is difficult to find a closed-form solution for the stationary point.14 To facilitate the derivation of the following imaging algorithm, we expand the signal phase by a power series with respect to , as follows: where where is the carrier frequency and , , and are the Doppler parameters of the echo signal, given byFrom Eqs. (15) to (17), it can be seen that the Doppler parameters , , and vary with range , which increases the difficulty for the following imaging process. Figure 2 shows the curve of the Doppler parameters with respect to slant range displacement. There is a nearly linear relationship between the Doppler parameters and the range displacement. To describe the range dependence of the Doppler parameters, a linear hypothesis is used to deduce the following imaging algorithm, which is given by Substituting Eqs. (18) into (10), the PTS based on the MESRM can be obtained, and the corresponding improved imaging algorithm is presented in the following section. 3.Higher Order Chirp Scaling AlgorithmBased on the proposed signal model in Sec. 2, an improved imaging algorithm is presented here: higher order cross-coupling is removed by higher order phase compensation, the accurate range cell migration correction (RCMC) and secondary range compressed (SRC) are accomplished by the improved CS processing, and accurate azimuth focusing is achieved through the range-dependent azimuth-matched filtering. The block diagram of our proposed algorithm is shown in Fig. 3. In the following, details of the basic operations are provided according to the signal flow in the diagram. It starts with higher order phase compensation and cubic phase filtering in the 2-D frequency domain, where cubic phase filtering is used to provide the most accurate accommodation of range dependence of SRC, and the higher order cross-coupling is removed by the higher order phase compensation. The higher order phase function and cubic phase function are given by where is the azimuth-frequency varying cubic phase filter coefficient, given byAfter higher order phase compensation and cubic phase filtering, the signal is transformed into the range-Doppler domain by range inverse FFT (IFFT). Considering that the cubic phase term is small enough, the range-Doppler domain representation of the filtered signal can then be written as whereTo remove the range dependence of SRC and RCM, NLCS processing is performed, where the NLCS function , centered at the reference range , is given by where and denote the quadratic and cubic coefficientsAfter NLCS processing, the signal can be expressed as whereFrom Eq. (30), it can be seen that the RCMC and SRC are independent of range , and the bulk RCMC and SRC can be performed accurately and efficiently across the range swath. Accordingly, the range processing filter is given by After the range IFFT takes the data back to the range-Doppler domain, range-dependent azimuth-matched filtering and residual phase compensation can be performed by the azimuth processing filter Finally, a well-focused target is generated by the azimuth IFFT. 4.Simulations and AnalysesNow, simulations are performed to first validate the MESRM for MEO SAR. Then, the accuracy of the derived 2-D spectrum is verified with a different azimuth resolution. Finally, the performance of our proposed imaging algorithm is demonstrated. The simulation parameters are listed in Table 1. Table 1Simulation parameters for modified equivalent squint range model (MEO SAR).
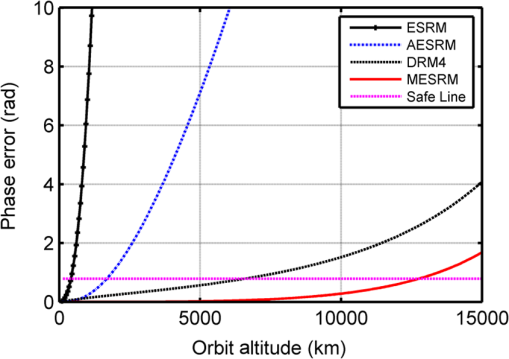
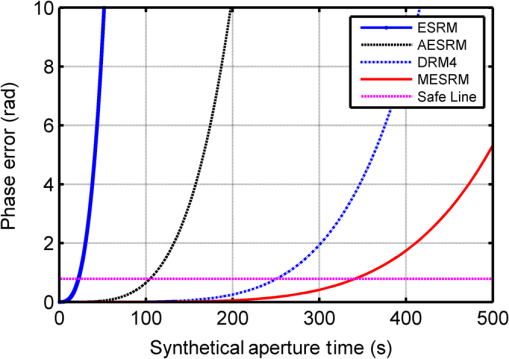
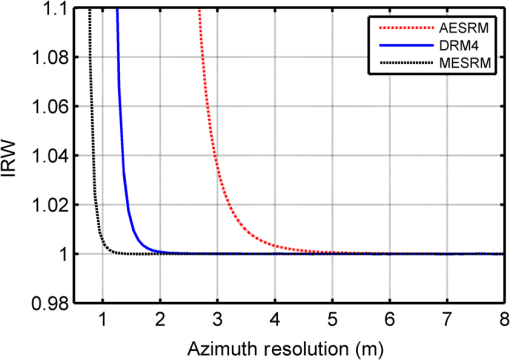
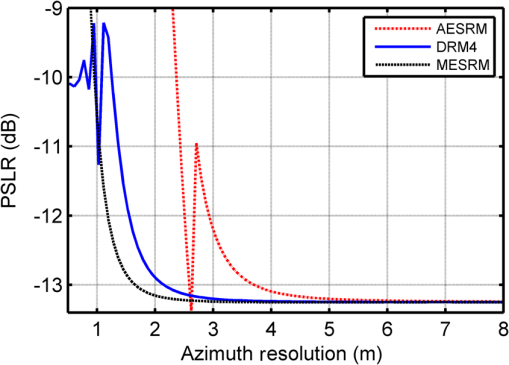
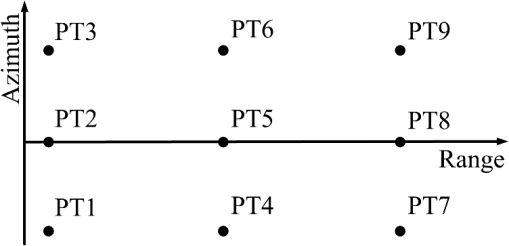
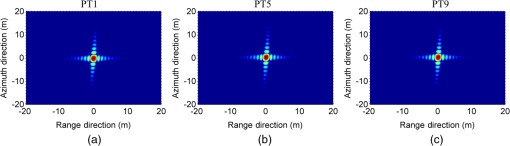
4.1.Simulation for Modified Equivalent Squint Range ModelThe capability of a given range model is mainly determined by the azimuth phase error. To show the accuracy of the MESRM, the azimuth phase errors caused by range deviation as a function of orbit altitude are provided in Fig. 4, where the azimuth resolution is set to be 1.5 m, and the other parameters are listed in Table 1. It can be clearly seen that the MESRM is more accurate than the ESRM, AESRM, and DRM4. Under the azimuth phase criterion of , MESRM performs very well up to 12,000 km, whereas the performance of the AESRM degrades dramatically above 1700 km. Figure 5 illustrates the phase errors caused by range deviation as a function of the synthetic aperture time. It is shown that, under the azimuth phase error criterion of , the maximal synthetic aperture time for MESRM is up to 300 s. As a result, an azimuth resolution higher than 1.5 m can be achieved. 4.2.Simulation for Two-Dimensional SpectrumThe 2-D PTS is the basis of an imaging algorithm. To verify the accuracy of the 2-D spectrum, we compress the echo signal with the 2-D spectrum based on MESRM, AESRM, and DRM4. The impulse response widths (IRWs) (normalized to the theoretical value) and the peak sidelobe ratio (PSLR) with respect to azimuth resolution are plotted in Figs. 6 and 7, respectively. It can be seen that the 2-D spectrum can maintain sufficient accuracy even if the azimuth resolution is up to 1.5 m, where the deterioration of IRWs is less than 1% and the degradation of PSLR is less than 0.4 dB, which can meet the requirements of MEO SAR. 4.3.Simulation for AlgorithmTo demonstrate the performance of the proposed imaging algorithm, raw data are first generated in our simulation for point targets using the parameters given in Table 1, with the scene shown in Fig. 8. The distances of different targets along the range and azimuth are 40.0 and 0.6 km, respectively. Moreover, rectangular weighting is used for both azimuth and range processing. The focused result of the NLCS algorithm is shown in Fig. 9 for comparison, where the HREM is used and the corresponding parameters are calculated for each range bin. It can be seen that the focused results suffer from severe degradation, and significant azimuth mainlobe broadening and sidelobe rising are observed for all targets. Figure 10 shows the focused result based on our proposed algorithm. The interpolated contours of PT1, PT5, and PT9 are presented in Fig. 11 to evaluate the image quality. Compared to the NLCS algorithm result, the focusing performance has been significantly improved. To quantify the focusing performance, the point target analysis results are listed in Table 2, where the subscript represents the measured value, and represents the calculated value. The ideal PSLR and the integrated sidelobe ratio (ISLR) are 13.26 and 9.68 dB, respectively, using the rectangular window. Table 2Performance analysis of point targets.
According to Table 2, it can be seen that the deterioration of IRW in the range direction is less than 1% and that in the azimuth direction is less than 1.5%. The PSLRs and ISLRs have less than 5% degradation in both the azimuth and range directions. All these indicate that the corresponding focusing algorithm can effectively meet the imaging requirement of the MEO SAR. Location is another index with which to evaluate the performance of imaging algorithms. Table 3 shows position deviations of all targets after being compressed, where the slant-range imaging plane is taken as the reference. We can see that position deviation in both the range and azimuth directions is less than 0.3 m, showing a high location accuracy for our proposed algorithm. Table 3Location results of point targets.
5.ConclusionFor MEO spaceborne SAR, an improved higher order NLCS algorithm based on MESRM has been proposed in this paper, which takes into account the curved orbit and the range dependence of the PTS. Based on the MESRM, the corresponding signal model as well as the PTS have been derived. A modified higher order imaging algorithm has also been developed, where higher order phase compensation is introduced to remove higher order cross-coupling, and accurate focusing is achieved by the improved NLCS algorithm. Simulation results have been provided to verify the effectiveness of the proposed model and the corresponding imaging algorithm. AppendicesAppendix:Derivation of Two-Dimensional Point Target SpectrumTo derive the 2-D PTS of the echo signal, we first expand the range model by power series with respect to Applying the series reversion in Eq. (9)15 yields the following 2-D spectrum whereNext,we expand the signal phase by power series with respect to , as follows: Finally, we merge with , and the 2-D PTS in Eq. (10) can be obtained. AcknowledgmentsThis work was supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 61132006 and 61171123. ReferencesJ. C. Curlander and R. N. McDonough, Synthetic Aperture Radar: Systems and Signal Processing, Wiley, New York, New York
(1991). Google Scholar
W. Townsend,
“An initial assessment of the performance achieved by the Seasat-1 radar altimeter,”
IEEE J. Ocean. Eng., 5
(2), 80
–92
(1980). http://dx.doi.org/10.1109/JOE.1980.1145459 IJOEDY 0364-9059 Google Scholar
D. L. Evans et al.,
“Seasat—a 25-year legacy of success,”
Remote Sens. Environ., 94
(3), 384
–404
(2005). http://dx.doi.org/10.1016/j.rse.2004.09.011 RSEEA7 0034-4257 Google Scholar
A. Moussessian et al.,
“System concepts and technologies for high orbit SAR,”
in Proc. IEEE MTT-S Int. Microw. Symp.,
1623
–1626
(2005). Google Scholar
D. M. Tralli, W. Foxall and C. Schultz,
“Concept for a high MEO InSAR seismic monitoring system,”
in Proc. IEEE Aerosp. Conf.,
1
–7
(2007). Google Scholar
J. Mittermayer, A. Moreira and O. Loffeld,
“Spotlight SAR data processing using the frequency scaling algorithm,”
IEEE Trans. Geosci. Remote Sens., 37
(5), 2198
–2214
(1999). http://dx.doi.org/10.1109/36.789617 IGRSD2 0196-2892 Google Scholar
X. Sun et al.,
“Time-varying step-transform algorithm for high squint SAR imaging,”
IEEE Trans. Geosci. Remote Sens., 37
(6), 2668
–2677
(1999). http://dx.doi.org/10.1109/36.803414 IGRSD2 0196-2892 Google Scholar
K. Eldhuset,
“A new fourth-order processing algorithm for spaceborne SAR,”
IEEE Trans. Aerosp. Electron. Syst., 34
(3), 824
–835
(1998). http://dx.doi.org/10.1109/7.705890 IEARAX 0018-9251 Google Scholar
K. Eldhuset,
“Ultra high resolution spaceborne SAR processing,”
IEEE Trans. Aerosp. Electron. Syst., 40
(1), 370
–378
(2004). http://dx.doi.org/10.1109/TAES.2004.1292176 IEARAX 0018-9251 Google Scholar
L. Huang et al.,
“Focusing of medium-earth-orbit SAR with advanced nonlinear chirp scaling algorithm,”
IEEE Trans. Geosci. Remote Sens., 49
(1), 500
–508
(2011). http://dx.doi.org/10.1109/TGRS.2010.2053211 IGRSD2 0196-2892 Google Scholar
Y. Neo, F. H. Wong and I. G. Cumming,
“A comparison of point target spectra derived for bistatic SAR processing,”
IEEE Trans. Geosci. Remote Sens., 46
(9), 2481
–2492
(2008). http://dx.doi.org/10.1109/TGRS.2008.919018 IGRSD2 0196-2892 Google Scholar
P. B. Wang et al.,
“A high-order imaging algorithm for high-resolution spaceborne SAR based on a modified equivalent squint range model,”
IEEE Trans. Geosci. Remote Sens., 53
(3), 1125
–1135
(2015). http://dx.doi.org/10.1109/TGRS.2014.2336241 IGRSD2 0196-2892 Google Scholar
R. K. Raney et al.,
“Precision SAR processing using chirp scaling,”
IEEE Trans. Geosci. Remote Sens., 32
(4), 786
–799
(1994). http://dx.doi.org/10.1109/36.298008 IGRSD2 0196-2892 Google Scholar
G. W. Davidson, I. G. Cumming and M. R. Ito,
“A chirp scaling approach for processing squint mode SAR data,”
IEEE Trans. Aerosp. Electron. Syst., 32
(1), 121
–133
(1996). http://dx.doi.org/10.1109/7.481254 IEARAX 0018-9251 Google Scholar
Y. Neo, F. H. Wong and I. G. Cumming,
“A two-dimensional spectrum for bistatic SAR processing using series reversion,”
IEEE Geosci. Remote Sens. Lett., 4
(1), 93
–96
(2007). http://dx.doi.org/10.1109/LGRS.2006.885862 IGRSBY 1545-598X Google Scholar
BiographyPengbo Wang received his PhD degree in information and communication engineering from Beihang University, Beijing, China, in 2007. Since July 2010, he has been with the school of Electronics and Information Engineering, Beihang University (BUAA), as a lecturer. His current research interests include high-resolution spaceborne synthetic aperture radar (SAR) image formation, novel techniques for spaceborne SAR systems, and multimodal remote sensing data fusion. Wei Liu received his PhD degree in 2003 from the School of Electronics and Computer Science, University of Southampton, United Kingdom. Since September 2005, he has been with the Communications Research Group, Department of Electronic and Electrical Engineering, University of Sheffield, United Kingdom, as a lecturer. His research interests include sensor array signal processing, blind signal processing, multirate signal processing and their various applications in wireless communications, sonar, radar, satellite navigation, speech enhancement, and biomedical engineering. Jie Chen received his BS and PhD degrees from Beihang University, China, in 1996 and 2002, respectively. He is a professor with the School of Electronics and Information Engineering, Beihang University (BUAA) from 2004. His current research interests include remote sensing information acquisition and signal processing, topside ionosphere exploration based on spaceborne HF-SAR, high-resolution spaceborne SAR image formation, and modeling and simulation for spaceborne SAR systems. Wei Yang received his MS and PhD degrees from Beihang University, China, in 2008 and 2011, respectively. He has been a lecturer with the School of Electronics and Information Engineering, Beihang University, since 2013. His current research interests include high-resolution spaceborne SAR image formation and modeling and simulation for spaceborne SAR systems. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||