|
|
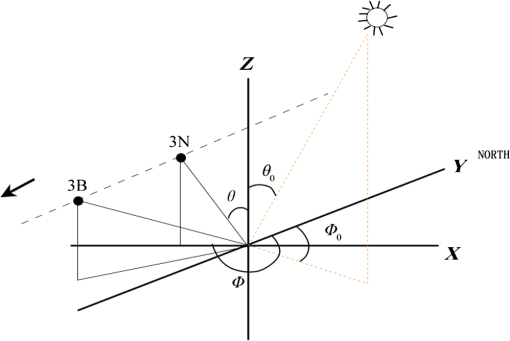
1.IntroductionRemote sensing of ocean bottom topography is an important research area that is significant for sea floor mapping and submarine object detection.1,2 Shallow water bathymetry features were first discovered on radar images in 1969.3,4 Since then, numerous studies have found that under low-to-moderate wind and strong tidal current conditions, real aperture radar and synthetic aperture radar (SAR) can detect bottom topography features in both shallow1,5–7 and deep waters.2 One-dimensional (1-D) SAR imaging of shallow water bottom topography was first proposed by Alpers and Hennings,8 and a theoretical model was provided.8,9 Many researchers have subsequently studied ocean topography in SAR images worldwide. For example, Vogelzang et al.10,11 performed experiments to study the imaging of bottom topography with polarimetric P-, L-, and C-band SAR. Fu et al.12 studied SAR imaging mechanisms of sea bottom topography and analyzed the relationship between topographic parameters and SAR mapping of sea bottom topography. Yang et al.13 developed a detection model for underwater topography with a series of SAR images acquired at different times by combining the model with tide and tidal-current numerical simulations. Sun glitter remote sensing is another remote sensing method based on variations in sea surface roughness (SSR). Cox and Munk14 developed the well-known mathematical relationship between sun glitter radiance and the probability distribution of the reflecting facets’ slope, allowing the surface to be observed (the Cox-Munk model). The Cox–Munk model established a fundamental theory enabling sun glitter images to detect marine dynamic processes, and sun glitter remote sensing has played an important role in a wide range of oceanographic studies, including internal wave detection,15,16 oil slick detection,17 and shallow underwater topography mapping.7,18 Hennings et al.19 developed a key theory of the sun glitter imaging mechanisms for underwater bottom topography based on the Cox-Munk model and SAR imaging mechanisms. He et al.,20 Shao et al.,21 and Zhang et al.22 used sun glitter imagery to observe sand waves in the Taiwan Banks, and statistically analyzed their distributions and characteristics. According to the sun glitter geometry model, it has been found that the signature of sun glitter images depends strongly on the viewing angle.19,23,24 He et al.25 discussed the brightness reversal of the Taiwan Banks submarine sand waves in sun glitter images from charge-coupled diodes onboard the HJ-1B satellite. Therefore, multiangle sun glitter images can present useful additional information compared with single angle images. Chust and Sagarminaga26 tested the use of the multiangle imaging spectroradiometer (MISR) for detecting oil spills in Lake Maracaibo, and found that the MISR sensor has an improved capability for oil spill discrimination compared with the single-view moderate resolution imaging spectroRadiometer sensor. Matthews27 utilized the nadir and back-looking views of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) to detect internal waves and ship wakes, and he also proposed a “Back to Nadir” ratio to estimate SSR, In addition, he suggested that more information could be extracted from multiangle data. However, bathymetric mapping of submarine topography using multiangle sun glitter images has not yet been explored. In this paper, we present a method for bathymetric mapping of submarine sand waves using multiangle sun glitter imagery. The study area and data are introduced in the Sec. 1. Then, the methodology, including multiangle sun glitter geometry, a sun glitter image model, and a depth retrieval method are presented. Finally, a case study and its calculation results are discussed. 2.Study Area and Data2.1.Study AreaThe study area is located in the Taiwan Banks, at the southern entrance of the Taiwan Strait. In this region, sand waves in shallow water shoals (namely, the Taiwan Banks) are characterized by large wave heights.28,29 Covering a total area of approximately , the Taiwan Banks extend west–east (from Dongshan Island and the Fujian coast region to the Penghu Islands),22 centered at 23°00’N, 118°30’E. Water depths in the Taiwan Banks are relatively shallow, ranging from 10 to 35 m, with an average depth of 20 m. Owing to the input of coastal sediments and nonferrous materials, the highest water optical transparency is only about 30 m, while in the nearshore, zone values range from just 2 to 10 m.30 Therefore, it is difficult for visible solar radiance to reach the marine bottom, making it particularly difficult to identify seafloor bathymetry using remote sensing methods. However, the submarine sand waves are always visible using sun glitter images.31 2.2.Satellite Imagery and Sounding DataASTER is an advanced multispectral imager onboard the NASA’s Terra spacecraft that was launched in December 1999. The ASTER instrument consists of three separate instrument subsystems: the visible and near-infrared (VNIR), the shortwave infrared, and the thermal infrared sensors. The VNIR sensor has three bands with a spatial resolution of 15 m, and an additional backward telescope for stereo observation. Channel 3N at nadir has the same bandwidth (0.78 to for near-infrared), and channel 3B has a back-looking view that detects the same region after 55 s. Initially, the stereo imaging mode was designed for the terrestrial sciences, e.g., for generating high-accuracy digital elevation models. However, for sun glitter investigations, the high spatial resolution (15 m), the sensor tilt capability, and the back-looking view from channel 3B, mean that ASTER has considerable potential for multiangle ocean remote sensing. Figure 1(a) shows the nadir view image (NVI) imaged by channel 3N of the VNIR sensor in the study area on July 16, 2003, at 02:47:27 UTC. Most of the sand waves are well-defined in the high-quality image, with dark and bright strips clearly visible. However, the brightness of the entire image increases from west to east, suggesting a matching tendency in the sun glitter radiance. Figure 1(b) is the back-looking view image (BVI) gathered by channel 3B of the VNIR sensor, obtained after 55 s for the same area. Relative to the NVI, the brightness of the BVI descends smoothly over the entire image. The tidal flow-field of the sea surface was obtained using a numerical calculation model. At the time the images were captured, the tidal flow direction, which was almost perpendicular to the sand-wave-crest orientation was from south to north with speed of . Fig. 1Stereo images acquired on July 16, 2003, at 02:47:27 UTC by Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) on board NASA’s Terra satellite. (a) Nadir view image (NVI) and (b) back-looking view image (BVI). The red lines labeled A, B, and C denote the profiles presented in Fig. 3.  The bathymetric data used in this study was obtained by the R2Sonic 2024 broadband multibeam echo sounder device using the fifth generation multibeam architecture. The device can be used in submarine bathymetry surveys in the range of 1 to 500 m. Its frequency range is from 200 to 400 kHz, selectable swath coverage is from 10 deg to 160 deg, beam angle is with 256 efficient beams, and resolution is 1.25 cm. The sounding data for this study was obtained from May 25, 2012, to June 28, 2012, and has data spacing for two adjacent points of 10 m. 3.MethodologyAccording to Hennings et al.,19 the mechanism of sun glitter imaging for bottom topography is similar to that for SAR imaging described by Alpers and Hennings.8 The difference is that the Bragg resonant scattering model is replaced by the Cox–Munk model14 to express variations in the SSR shown by sun glitter images. The mechanism includes three processes:19 (1) interactions between sea bottom topography and the current cause modulations in the surface current velocity; (2) modulations in the surface current cause variations in the spectrum of surface short waves that determine the SSR; (3) variations in the SSR show in sun glitter images. However, the imaging geometry is a critical issue for stereo sun glitter remote sensing. Therefore, we first introduce the stereo sun glitter geometry and develop a method for determining the imaging geometry of each pixel. Then we introduce the mechanisms for modeling sun glitter imaging of submarine sand waves. Finally, we present a new method for retrieving the water depth of sand waves using the stereo sun glitter images. 3.1.Multiangle Sun Glitter GeometryThe header file of the ASTER image only provides two angles: the pointing angle () and the scene orientation angle (). However, previous researchers have generally used and to identify the entire image. Matthews27 discusses sun glitter geometry in the nadir and back-looking view ASTER images, but his calculation focuses on only one side of the nadir, whereas angles may change when the ASTER image is acquired from both sides of the nadir. Yang et al.32 provided an improved treatment of the sun glitter geometry of each pixel in ASTER imagery. Figure 2 shows the observational geometry for sun glitter in ASTER stereo image pairs. The sun zenith angle () and the sun azimuth angle () of each pixel can be determined by its position and imaging time. The view angle and the sensor zenith angle in the nadir view are and , respectively, and the view angle and the sensor zenith angle in the back-looking view are and , respectively.32 The view angle in the NVI is given by where denotes the pixel number from the sensor center, IFOV is instantaneous field of view, and denotes the pointing angle of the image.The sensor zenith angle in the nadir view is given by where denotes the scene orientation angle of the image.The view angle in the BVI becomes where denotes the satellite height (m), denotes the spatial resolution of the VNIR sensor (15 m), and denotes the angle between the nadir view and the back-looking view (27.6 deg for the VNIR sensor).We can obtain the sensor zenith angle in BVI () as where is the base-to-height within the stereo image pair (0.6 for ASTER stereo images).3.2.Sun Glitter Imaging ModelIn this study, the absolute value of radiance is not considered because only the variation of the reflectance caused by SSR is of interest. Therefore, normalized sun glitter radiance, , given by Gordon is adopted in this study.33 The angle of reflection is , denotes the tilt angle of the wave facet, denotes the Fresnel reflection coefficient; they are calculated from the sensor view angle (), the sensor zenith angle (), the sun zenith angle (), and the sun azimuth angle (). is the probability density function (PDF) as functions of individual slope components and . In this study, the isotropic PDF (independence with wind direction) is used according to the Cox and Munk model,14 and it is given by where denotes the SSR, denotes the wind-generated SSR (background roughness), and denotes the variation of SSR modulated by the interaction of current and bottom topography. There are several empirical expressions of as the function of wind speed, but the Cox–Munk model was testified to have the best performance by Zhang and Wang.24 The variation of SSR, , is given by where is the wave number of short gravity waves, is the lower wave number limit that produces sun glitter radiance modulation, and is the maximum wave number where the effect of surface tension is negligible. According to Hennings et al.,19 , and . denotes the modulation of the spectral energy density of waves and is given by where denotes the relationship between group velocity and phase velocity of short waves; for gravity waves, . denotes the relaxation rate. According to Shao et al.,31 is approximately for the Taiwan Banks. denotes the spectral energy density of waves, and denotes the current velocity gradient. The spectral energy density is given by where is the Phillips constant (0.004).Inserting Eqs. (8) and (9) into Eq. (7) gives 3.3.Depth Retrieval MethodIn order to calculate the SSR (), we directly calculate the ratio of the glitter radiance in the NVI to that in the BVI, based on Eqs. (5) and (6) where , , , and denote the normalized sun glitter radiance, the view angle, the Fresnel reflection coefficient, and the tilt angle of the wave facet, respectively, in the NVI, and , , and denote these parameters in the BVI. The SSR is given byBecause denotes the background roughness (wind-generated SSR), we consider that Therefore, is calculated by On this basis, we can obtain the variation of SSR () using stereo sun glitter images. To simplify Eq. (10), we suppose that the constant is given by On the basis of Eqs. (10) and (15), the current velocity gradient is given by Considering the current velocity along a transect perpendicular to a sand wave crest, it is possible to calculate the current velocity of each pixel site () by the following integration According to the Alpers–Hennings model,8 a 1-D model is used to describe the relationship between current velocity and water depth with the continuity equation where , , and are the mean (background) current velocity, the mean depth, and the local depth in the -direction perpendicular to submarine topography (e.g., the sand wave crest), respectively. and can be considered as constants for a sand wave. Therefore, if and are given or calculated using some true water depth data points, the water depth for the whole sand wave can be retrieved. In addition, , given by Eq. (15), is not sufficiently accurate because the parameters in Eq. (15), such as , , , , and , are determined using approximations. Therefore, is also not sufficiently accurate to give water depth. However, its relative values and varying trends can be used to estimate the relative depth of sand waves. Therefore, and can be set at any reasonable values ( and 20 m in this case, respectively) to calculate the relative depth of sand waves. Then some known true depths (at least two points, ideally one sited at the crest of the sand wave and another at the trough) are input to project the water depth of the whole sand wave.4.Results and DiscussionsFrom Figs. 1(a) and 1(b), three sites, labeled A, B, and C from west to east, were selected for water depth inversion. The profiles of image values (the pixel gray values) in the NVI and the BVI are plotted in Fig. 3, which shows that the curve trends for the NVI are almost exactly opposite to the BVI trends, indicating the brightness reversal due to the different view angles. For site A, the image values vary from 15.5 to 23.3 in the NVI, and from 5.2 to 9.5 in the BVI. Average values are 18.9 and 7.2 for the NVI and BVI, respectively. For site B, the average image values increase to 22.4 in the NVI and 7.4 in the BVI, and the image values vary from 19.0 to 26.7, and from 6.0 to 9.5 in the NVI and BVI, respectively. For site C, the average image values further increase to 28.3 in the NVI and 7.8 in the BVI, and the image values range from 23.3 to 34.5 in the NVI, and from 6.0 to 10.3 in the BVI. Thus, the average image values increase significantly from west to east in the NVI, varying by c. 50% (from 18.9 to 28.3), implying that the sand waves at the east site are more easily distinguished than those at the west site. However, no significant variations are seen in the BVI results from the three sites. Fig. 3Profiles of image pixel values and estimated sea surface roughness (SSR) at: (a) site A, (b) site B, and (c) site C (locations shown in Fig. 1). Blue curves denote the profiles of image pixel values for NVIs, red curves denote the profiles of image pixel values for BVIs, and green curves denote the SSR profiles. 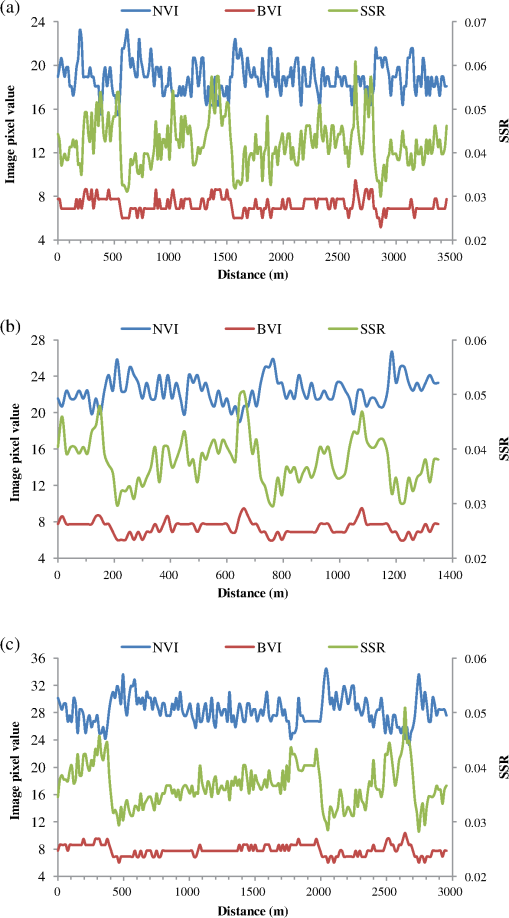 The pixel gray values are converted to radiance values by a radiation conversion transformation using the radiation parameters in the header file of the ASTER image. Then the radiance values and image geometric angles are input to calculate SSR for each pixel using Eq. (12). The SSRs of the three sites are shown by the green curves in Fig. 3, and range from 0.0300 to 0.0609, 0.02996 to 0.0506, and 0.0282 to 0.0509 at sites A, B, and C, respectively. The average SSR values are 0.0422, 0.0379, and 0.0367 for sites A to C, respectively. The variations seen in the SSR trend are contrary to those in the NVI values. However, the variation rate is only c. 15% less than that for the average image values in NVI (c. 50%). In addition, the SSR profiles show clearer bright–dark stripes than both the NVI and the BVI, indicating that multiangle images are more valuable than single angle images for bathymetric mapping. With the proposed method, and relative depth are calculated in turn based on the SSR. Five to six true depths from sounding datasets are then used to project the relative depth of each site. Among them, two true depths are used for each sand wave, separated according to the sand-wave morphology. The true depth data points are shown by arrows in Fig. 4, along with the inversion depths of the three sites. The associated accuracy evaluation results are shown in Fig. 5. The root-mean-square error (RMSE) and the correlation coefficient () between the inversion depths and the true depths are then calculated. The relative errors are also calculated as the ratio of the RMSE to the average water depth. The results from site A show that trend shapes of the inversion and the true depths match well [Fig. 4(a)], and their correlation coefficient is high (), although there are some significant differences in the details. The RMSE is 2.39 m and the relative error is 7.67%. Results from site B [Fig. 4(b)] and site C [Fig. 4(c)] both show good inversions with high correlation coefficients ( and ). The RMSE and relative error for site B are 2.46 m and 8.12%, respectively, and 1.45 m and 5.48% for site C. Fig. 4Results of water depth inversions at: (a) site A, (b) site B, and (c) site C, (locations shown in Fig. 1). Blue curves denote the retrieval depths, and red curves denote the sounding depths. Dashed lines denote the separation lines dividing the profiles into S1, S2, and S3 according to the sand-wave morphology for relative depth projections. Black arrows denote the true depth data points used to project relative depth, and only the points in each division (S1, S2, or S3) are used for projections in this division, except that P2 in (b) and (c) was used for both S1 and S2. 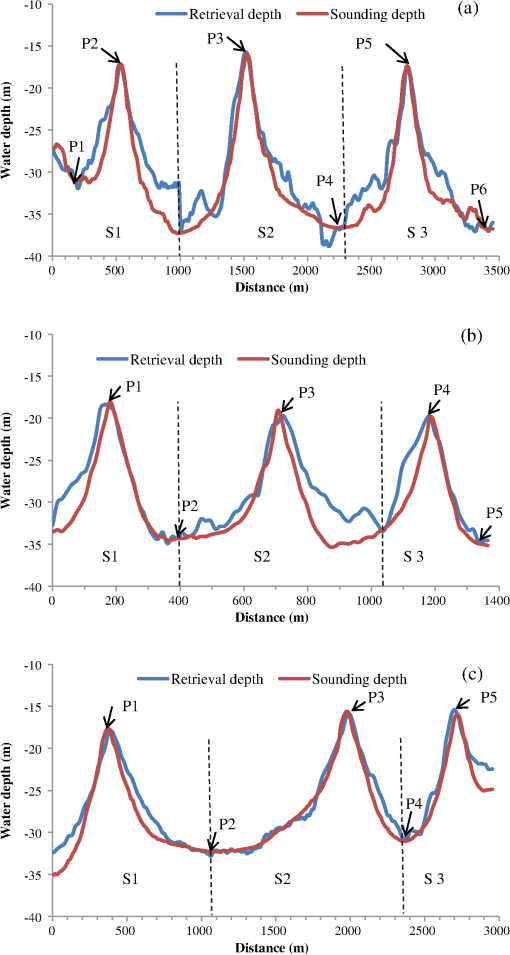 Fig. 5Accuracy evaluation results for retrieval depth compared with sounding depth at: (a) site A, (b) site B, and (c) site C. 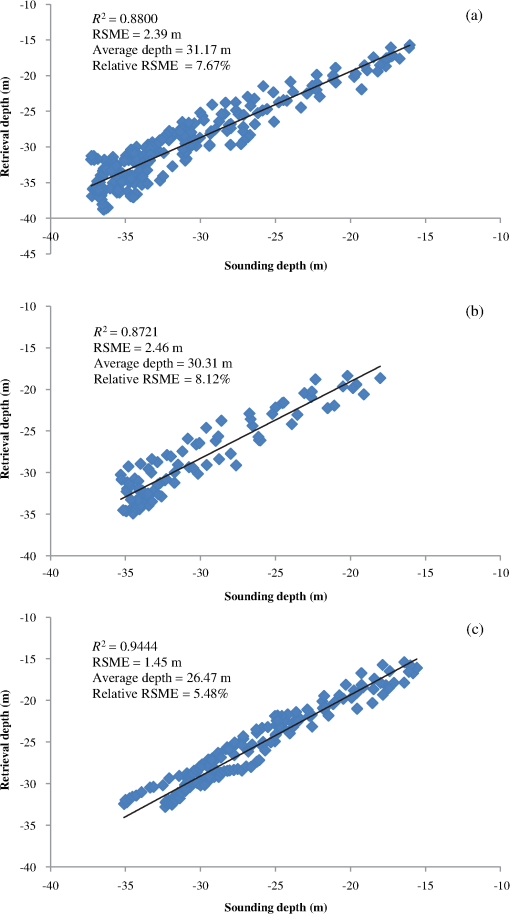 Although our results seem unconvincing compared with 30 cm results from the bathymetry assessment system (BAS) presented by Calkoen et al.,34 the water depth in the BAS case study was relatively low (c. 5 m) compared with the water depth (c. 31.0 m) in this study. Compared with the BAS study, this approach requires fewer true depths, does not require supporting environmental parameters, and the operation is relatively simple. Compared with results from He,20 our approach achieves a similar accuracy, but requires fewer true depths. Although Shao et al.21 presented an approach for mapping submarine sand waves that required only a few true depths, their technique is based on prior knowledge of sand wave morphology. In contrast, our approach requires no knowledge of the morphology, and the operation is simpler and does not involve an iterative process. In summary, the advantages of our proposed method include the requirement for fewer true depths, the fact that supporting environmental parameters and knowledge of the sand-wave morphology are not needed, and simpler operation. From the above analysis, given the acceptable accuracies, we conclude that this approach represents a significant improvement over previous methods. However, one limitation is that at least two view angle images simultaneously have distinguishable sun glitter information at the same time. 5.ConclusionsIn this paper, we present a new method for bathymetric mapping of submarine sand waves using stereo sun glitter images from the ASTER sensor. The results of our study yield a number of important conclusions as follows. Based on a multiangle image geometry model and a sun glitter radiance transfer model, a method for deriving SSR was developed using multiangle sun glitter images. Compared with methods that use single angle sun glitter data, our method avoids the dependence on observation angle. A water depth inversion method was developed based on the Alpers–Hennings model, with a few supporting true depth data points. The case study results show that the shapes of the trends for the inversion and the true depths (sounding data) are well matched, and their correlation coefficients are high (, , and ). The accuracy evaluation shows that the RMSE values range from 1.45 to 2.46 m, and that the relative errors range from 5.48% to 8.12%. Compared with previous research, our proposed method has equal or higher precision with several some advantages. The proposed method requires fewer true depth data, has no requirement for supporting environmental parameters or knowledge of sand-wave morphology, and is relatively simple to operate. Given the acceptable accuracies, we conclude that this approach represents a significant improvement over previous methods. We have shown that our method is effective in mapping submarine sand waves. It is also anticipated that this method can be used to map other types of submarine topography because the method is independent of terrain morphology. We consider that this method has significant potential in the observation of submarine topography, particularly with the operation of an increasing number of multiangle optical remote sensors. However, a limitation lies in that at least two view angle images simultaneously have distinguishable sun glitter information. We will conduct more case studies and improve the method. AcknowledgmentsThe stereo-optical images used in this study were provided by the Center for Earth Observation and Digital Earth, Chinese Academy of Sciences, China. The bathymetry data used in this study were obtained under the Public Science and Technology Research Fund Project of Ocean (Grant Number 201105001), and were processed by the Third Institute of Oceanography, State Oceanic Administration, China. This research was supported by the Project of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography (Grant Number SOEDZZ1513), the Public Science and Technology Research Fund Project of Surveying, Mapping and Geoinformation (Grant Number 201512030), and the Public Science and Technology Research Fund Project of Ocean (Grant Number 201105001). The authors would like to thank Editage for English language editing. ReferencesW. Alpers et al.,
“Underwater topography,”
Synthetic Aperture Radar Marine User’s Manual, 245
–262 US Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Serve, Office of Research and Applications, Washington DC
(2004). Google Scholar
X. F. Li et al.,
“Deep-water bathymetric features imaged by spaceborne SAR in the Gulf stream region,”
Geophys. Res. Lett., 37 L19603
(2010). http://dx.doi.org/10.1029/2010GL044406 GPRLAJ 0094-8276 Google Scholar
G. P. De Loor,
“Microwave measurements over the North Sea,”
Boundary Layer Meteorol., 13
(1–4), 119
–131
(1978). http://dx.doi.org/10.1007/BF00913866 Google Scholar
G. P. De Loor,
“The observation of tidal patterns, currents, and bathymetry with SLAR imagery of the sea,”
IEEE J. Oceanic Eng., 6
(4), 124
–129
(1981). http://dx.doi.org/10.1109/JOE.1981.1145501 IJOEDY 0364-9059 Google Scholar
X. F. Li et al.,
“Sea surface manifestation of along-tidal-channel underwater ridges imaged by SAR,”
IEEE Trans. Geosci. Remote Sens., 47
(8), 2467
–2477
(2009). http://dx.doi.org/10.1109/TGRS.2009.2014154 IGRSD2 0196-2892 Google Scholar
D. W. S. Lodge,
“Surface expression of bathymetry on SEASAT synthetic aperture radar images,”
Int. J. Remote Sens., 4
(3), 639
–653
(1983). http://dx.doi.org/10.1080/01431168308948580 IJSEDK 0143-1161 Google Scholar
W. Shi et al.,
“Ocean sand ridge signatures in the bohai sea observed by satellite ocean color and synthetic aperture radar measurements,”
Remote Sens. Environ., 115
(8), 1926
–1934
(2011). http://dx.doi.org/10.1016/j.rse.2011.03.015 Google Scholar
W. Alpers and I. Hennings,
“A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar,”
J. Geophys. Res., 89 10529
–10546
(1984). http://dx.doi.org/10.1029/JC089iC06p10529 Google Scholar
R. A. Shuchman et al.,
“Synthetic aperture radar imaging of ocean-bottom topography via tidal-current interactions: theory and observations,”
Int. J. Remote Sens., 6
(7), 1179
–1200
(1985). http://dx.doi.org/10.1080/01431168508948271 Google Scholar
J. Vogelzang et al.,
“Sea bottom topography with polarimetric P-, L- and C- band SAR,”
in Remote Sensing Science for the Nineties, 10th Annual Int. Geoscience and Remote Sensing Symp., 1990 (IGARSS’90),
2467
–2470
(1990). http://dx.doi.org/10.1109/IGARSS.1990.689040 Google Scholar
J. Vogelzang et al.,
“Mapping submarine sand waves with multiband imaging radar: experimental results and model comparison,”
J. Geophys. Res. Oceans, 102 1183
–1192
(1997). http://dx.doi.org/10.1029/96JC02836 Google Scholar
B. Fu et al.,
“Simulation study of sea bottom topography mapping by spaceborne SAR-Relationship between topographic parameters and measurement of water depth,”
Acta Oceanol. Sin., 23
(1), 35
–42
(2001). AOSIEE Google Scholar
J. G. Yang et al.,
“A detection model of underwater topography with a series of SAR images acquired at different time,”
Acta Oceanol. Sin., 29
(4), 28
–37
(2010). http://dx.doi.org/10.1007/s13131-010-0048-5 AOSIEE Google Scholar
C. Cox and W. Munk,
“Measurement of the roughness of the sea surface from photographs of the sun’s glitter,”
J. Opt. Soc. Am., 44
(11), 838
–850
(1954). http://dx.doi.org/10.1364/JOSA.44.000838 JOSAAH 0030-3941 Google Scholar
C. Jackson,
“Internal wave detection using the moderate resolution imaging spectroradiometer (MODIS),”
J. Geophys. Res. Oceans, 112
(C11), C11012
(2007). http://dx.doi.org/10.1029/2007JC004220 Google Scholar
B. Liu et al.,
“Tracking the internal waves in the South China Sea with environmental satellite sun glint images,”
Remote Sens. Lett., 5
(7), 609
–618
(2014). http://dx.doi.org/10.1080/2150704X.2014.949365 Google Scholar
C. M. Hu et al.,
“Detection of natural oil slicks in the NW Gulf of Mexico using MODIS imagery,”
Geophys. Res. Lett., 36 L10604
(2009). http://dx.doi.org/10.1029/2009GL037695 Google Scholar
I. Hennings et al.,
“Comparison of submarine relief features on a radar satellite image and on a Skylab satellite photograph,”
Int. J. Remote Sens., 9
(1), 45
–67
(1988). http://dx.doi.org/10.1080/01431168808954836 IJSEDK 0143-1161 Google Scholar
I. Hennings et al.,
“Sun glitter radiance and radar cross-section modulations of the sea bed,”
J. Geophys. Res., 99
(C8), 16303
–16326
(1994). http://dx.doi.org/10.1029/93JC02777 Google Scholar
X. K. He,
“Reconstruction of sand wave bathymetry using both satellite imagery and multi-beam bathymetric data: a case study of the Taiwan Banks,”
Int. J. Remote Sens., 35
(9), 3286
–3299
(2014). http://dx.doi.org/10.1080/01431161.2014.902551 IJSEDK 0143-1161 Google Scholar
H. Shao et al.,
“Priori knowledge based a bathymetry assessment method using the sun glitter imagery: a case study of sand waves on the Taiwan Banks,”
Acta Oceanol. Sin., 33
(1), 120
–126
(2014). http://dx.doi.org/10.1007/s13131-014-0375-z AOSIEE Google Scholar
H. G. Zhang et al.,
“Observation of sand waves in the Taiwan Banks using HJ-1A/1B sun glitter imagery,”
J. Appl. Remote Sens., 8
(1), 083570
(2014). http://dx.doi.org/10.1117/1.JRS.8.083570 Google Scholar
C. R. Jackson et al.,
“The role of the critical angle in brightness reversals on sunglint images of the sea surface,”
J. Geophys. Res., 115
(C9), C09019
(2010). http://dx.doi.org/10.1029/2009JC006037 Google Scholar
H. Zhang and M. H. Wang,
“Evaluation of sun glint models using MODIS measurements,”
J. Quant. Spectrosc. Radiat. Transfer, 111 492
–506
(2010). http://dx.doi.org/10.1016/j.jqsrt.2009.10.001 JQSRAE 0022-4073 Google Scholar
X. K. He et al.,
“The brightness reversal of submarine sand waves in ‘HJ-1A/B’ CCD sun glitter images,”
Acta Oceanolog. Sin., 34
(1), 94
–99
(2015). http://dx.doi.org/10.1007/s13131-015-0602-2 AOSIEE Google Scholar
G. Chust and Y. Sagarminaga,
“The multi-angle view of MISR detects oil slicks under sun glitter conditions,”
Remote Sens. Environ., 107
(1), 232
–239
(2007). http://dx.doi.org/10.1016/j.rse.2006.09.024 Google Scholar
J. Matthews,
“Stereo observation of lakes and coastal zones using ASTER imagery,”
Remote Sens. Environ., 99
(1), 16
–30
(2005)). http://dx.doi.org/10.1016/j.rse.2005.04.029 Google Scholar
S. Boggs,
“Sand-wave fields in Taiwan Strait,”
Geology, 2 251
–253
(1974). http://dx.doi.org/10.1130/0091-7613(1974)2<251:SFITS>2.0.CO;2 GLGYBA 0091-7613 Google Scholar
Z. C. Liu et al.,
“The development in the latest technique of shallow water multi-beam sounding system,”
Hydrographic Surv. Charting, 25 67
–70
(2005). Google Scholar
F. L. Li,
“Annual variations of Secchi depth in the near shore waters of the western Taiwan Strait during the summers of 1998–2010,”
J. Oceanogr. Taiwan Strait, 31
(3), 301
–306
(2012). Google Scholar
H. Shao et al.,
“Sun glitter imaging of submarine sand waves on the Taiwan Banks: determination of the relaxation rate of short waves,”
J. Geophys. Res., 116
(C6), C06024
(2011). http://dx.doi.org/10.1029/2010JC006798 Google Scholar
K. Yang et al.,
“Observation of submarine sand waves using ASTER stereo sun glitter imagery,”
Int. J. Remote Sens.,
(2015). http://dx.doi.org/10.1080/01431161.2015.1101652 Google Scholar
H. R. Gordon,
“Atmospheric correction of ocean color imagery in the earth observing system era,”
J. Geophys. Res., 102
(D14), 17081
–17106
(1997). http://dx.doi.org/10.1029/96JD02443 Google Scholar
C. J. Calkoen et al.,
“The bathymetry assessment system: efficient depth mapping in shallow seas using radar images,”
Int. J. Remote Sens., 22
(15), 2973
–2998
(2001). http://dx.doi.org/10.1080/01431160116928 IJSEDK 0143-1161 Google Scholar
BiographyHua-guo Zhang is an associate professor of the Second Institute of Oceanography, State Oceanic Administration, China. His research interest is the coastal remote sensing. He has published more than 20 papers. He received his BS degree in environment from Nankai University in 1999, his MS degree in oceanography at the Second Institute of Oceanography, State Oceanic Administration in 2002, and his PhD in oceanography from Ocean University of China in 2011. |